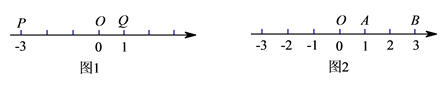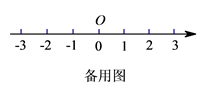安徽省合肥市包河区2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-02-03 类型：期中考试

进入出卷网下载

一、单选题

1. -5的相反数为（）．

A、 $- 5$ B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列各式中结果为负数的是（）

A、 $- (- 2)$ B、 $| - 2 |$ C、 ${(- 2)}^{2}$ D、 $- | - 2 |$

查看试题解析

3. 面粉厂规定某种面粉每袋的标准质量为

50 \pm 0.2

kg，现随机选取10袋面粉进行质量检测，结果如下表所示：

序号	1	2	3	4	5	6	7	8	9	10
质量（kg）	50	50.1	49.9	50.1	49.7	50.1	50	50	49.9	49.95

则不符合要求的有（）

A、1袋 B、2袋 C、3袋 D、4袋

查看试题解析

4. 下列各组式子中，不是同类项的是（）

A、 $3^{4}$ 与 $4^{3}$ B、 $- m n$ 与 $3 n m$ C、 $- 0.1 m^{2} n^{}$ 与 $\frac{1}{3} m^{2} n$ D、 $m^{2} n^{3}$ 与 $n^{2} m^{3}$

查看试题解析
5. 化简（-2x²+3x-2）-（-x²+2）正确的是（）

A、-x²+3x B、-x²+3x-4 C、-3x²-3x-4 D、-3x²+3x

查看试题解析
6. 如图，数轴上的A，B两点所表示的数分别是a，b，如果 $| a | > | b |$ ，且 $a b > 0$ ，那么该数轴的原点O的位置应该在（）

A、点A的左边 B、点B的右边 C、点A与点B之间靠近点A D、点A与点B之间靠近点B

查看试题解析
7. 如果|x﹣2|+（y+3）²=0，那么y ^x的值为（）

A、9 B、﹣9 C、6 D、﹣6

查看试题解析
8. 某商品每件成本 $a$ 元，按高于成本 $20%$ 的定价销售后滞销，因此又按售价的九折出售，则这件商品还可盈利（）

A、 $8 % a$ 元 B、 $10 % a$ 元 C、 $18 % a$ 元 D、 $20 % a$ 元

查看试题解析
9. 如果有理数 $a,b,c$ 满足关系式 $a<b<0<c$ ，那么代数式 $\frac{b c - a c}{a b^{2} c^{3}}$ 的值（）

A、必为正数 B、必为负数 C、可正可负 D、可能为0

查看试题解析
10. 观察下列各等式：
$- 2 + 3 = 1$

$-5-6+7+8=4$

$-10-l1-12+13+14+15=9$

$-17-18-19-20+21+22+23+24=16$

……

根据以上规律可知第11行左起第11个数是（）

A、-130 B、-131 C、-132 D、-133

查看试题解析

二、填空题

11. 若2是关于x的一元一次方程2x=kx+6的解，则k=

查看试题解析
12. 比较大小： $- (+ \frac{2}{3})$ $+ (- \frac{3}{4})$

查看试题解析
13. 计算： $- 3 \div (- \frac{1}{3}) \times 3$ = ．

查看试题解析
14. 写出一个只含有字母x的二次三项式．

查看试题解析
15. 若a﹣b＝2，ab＝﹣1，则b﹣a﹣2ab的值为．

查看试题解析
16. 有依次排列的 $3$ 个数：3，9，8对任相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，-1，8这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，-10，-1，9，8，继续依次操作下去，问：从数串3，9，8开始操作第 $2020$ 次以后所产生的那个新数串的所有数之和是．

查看试题解析

三、解答题

17. 计算：

(1)、 $(- \frac{1}{2}) \times (- 8) + {(- 6)}^{2}$

(2)、 $- 1^{^{4}} + (- 2) \div (+ \frac{1}{3}) + | - 9 |$

查看试题解析
18. 解方程：

(1)、 $3(2x-1)=15$

(2)、 $\frac{x - 2}{3} - \frac{1 + x}{2} = - 2$

查看试题解析
19. 小虫从点O出发在一条直线上来回爬行，向右爬行的路程记为正，向左爬行的路程记为负，爬行的各段路程依次为：+5，-3，+10，-8，-6，+12，-10(单位： $cm$ )

(1)、小虫最后是否回到出发点O？为什么？

(2)、小虫离开O点最远时是 $cm$ .

(3)、在爬行过程中，如果每爬行1 $cm$ 奖励1粒芝麻，则小虫一共可以得到多少粒芝麻？

查看试题解析
20. 先化简，再求值： ${2(a}^{2} {b+ab}^{2} {)-2(a}^{2} {b-1)-ab}^{2} -2$ ，其中 $a=1,b=-3 .$

查看试题解析
21. 设 ${A=x}^{3} {-2x}^{2} +4x+3$ ， ${B=x}^{2} +2x-6$ ， ${C=x}^{3} +2x-3$ ．当 $x=-2$ 时，求A-（B+C）的值．

查看试题解析
22. 对于数轴上的两点P，Q给出如下定义： P，Q两点到原点O的距离之差的绝对值称为P，Q两点的绝对距离，记为 $‖ P O Q ‖$ ．

例如：P，Q两点表示的数如图1所示，则 $‖ P O Q ‖ = | P O - Q O | = | 3 - 1 | = 2$ ．

(1)、A，B两点表示的数如图2所示．
①求A，B两点的绝对距离；

②若C为数轴上一点（不与点O重合），且 $‖ A O B ‖ = 2 ‖ A O C ‖$ ，求点C表示的数；

(2)、M，N为数轴上的两点（点M在点N左边），且MN=2，若 $‖ M O N ‖ = 1$ ，直接写出点M表示的数．

查看试题解析