河北省石家庄市平山县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-02-03 类型:期中考试
一、单选题
-
1. 下列交通标志中,是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中能够说明 是( )A、
2. 下列图形中能够说明 是( )A、 B、
B、 C、
C、 D、
D、 3. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、114. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)5. 利用尺规进行作图,根据下列条件作三角形,画出的三角形不是唯一的是( )A、已知三条边 B、已知三个角 C、已知两角和夹边 D、已知两边和夹角6. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则错误的结论是( )
3. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、114. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)5. 利用尺规进行作图,根据下列条件作三角形,画出的三角形不是唯一的是( )A、已知三条边 B、已知三个角 C、已知两角和夹边 D、已知两边和夹角6. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则错误的结论是( ) A、∠1=∠2 B、∠A=∠2 C、△ABC≌△CED D、∠A与∠D互为余角7. 下列命题:①三角形的三边长确定后,三角形的形状就唯一确定;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性,而四边形不具有稳定性.其中假命题的个数是( )A、1 B、2 C、3 D、48. 如图,已知 , 为 的中点,若 , ,则 为( )
A、∠1=∠2 B、∠A=∠2 C、△ABC≌△CED D、∠A与∠D互为余角7. 下列命题:①三角形的三边长确定后,三角形的形状就唯一确定;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性,而四边形不具有稳定性.其中假命题的个数是( )A、1 B、2 C、3 D、48. 如图,已知 , 为 的中点,若 , ,则 为( )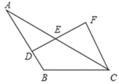 A、 B、 C、 D、9. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A、 B、 C、 D、9. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )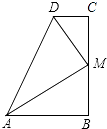 A、30° B、35° C、45° D、60°10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、30° B、35° C、45° D、60°10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )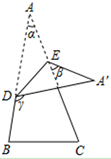 A、 B、 C、 D、11. 如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′的度数是( )
A、 B、 C、 D、11. 如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′的度数是( )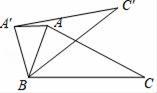 A、40° B、35° C、55° D、20°12. 如图,已知 ,点 、 、 …在射线 上,点 、 、 …在射线 上; 、 、 …均为等边三角形.若 ,则 的边长为( )
A、40° B、35° C、55° D、20°12. 如图,已知 ,点 、 、 …在射线 上,点 、 、 …在射线 上; 、 、 …均为等边三角形.若 ,则 的边长为( ) A、4040 B、 C、4042 D、
A、4040 B、 C、4042 D、二、填空题
-
13. 已知等腰三角形中的一条边长为2cm,另一条边长为5cm,则它的周长是cm.14. 如图,△OAD≌△OBC,且∠O=58°,∠C=20°,则∠OAD=°.
 15. 若一个多边形的内角和等于720度,则这个多边形的边数是16. 如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为 .
15. 若一个多边形的内角和等于720度,则这个多边形的边数是16. 如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为 . 17. 已知三角形ABC的三边长分别是 ,化简 的结果是;18. 如图,四边形ABCD中,∠BAD=136°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为度.
17. 已知三角形ABC的三边长分别是 ,化简 的结果是;18. 如图,四边形ABCD中,∠BAD=136°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为度.
三、解答题
-
19. 已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF.
 20. 如图, 是等腰三角形, , .
20. 如图, 是等腰三角形, , .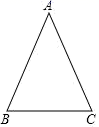 (1)、尺规作图:作 的角平分线 ,交 于点 (保留作图痕迹,不写作法);(2)、判断 是否为等腰三角形,并说明理由.21. 的三个顶点在边长为1的正方形网格中,已知 , , .
(1)、尺规作图:作 的角平分线 ,交 于点 (保留作图痕迹,不写作法);(2)、判断 是否为等腰三角形,并说明理由.21. 的三个顶点在边长为1的正方形网格中,已知 , , . (1)、画出 及关于 轴对称的 ;(2)、写出点 的对应点 的坐标是 , 点 的对应点 的坐标是 , 点 的对应点 的坐标是 .(3)、请直接写出以 为边且与 全等的三角形的第三个顶点(不与 重合)的坐标是 .22. 如图,在 中, , , 是 边的中线,过点 作 ,垂足为点 ,过点 作 交 的延长线于点 .
(1)、画出 及关于 轴对称的 ;(2)、写出点 的对应点 的坐标是 , 点 的对应点 的坐标是 , 点 的对应点 的坐标是 .(3)、请直接写出以 为边且与 全等的三角形的第三个顶点(不与 重合)的坐标是 .22. 如图,在 中, , , 是 边的中线,过点 作 ,垂足为点 ,过点 作 交 的延长线于点 . (1)、试说明 ;(2)、若 ,求 的长.23. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)、试说明 ;(2)、若 ,求 的长.23. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.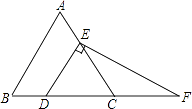 (1)、求∠F的度数;(2)、若CD=2,求DF的长.24. 如图,在 中, , , 为 的中点.
(1)、求∠F的度数;(2)、若CD=2,求DF的长.24. 如图,在 中, , , 为 的中点. (1)、写出 点到 的三个顶点 的距离关系.(2)、如果点 分别在线段 上移动,移动中保持 ,请写出 的形状,并证明你的结论.25. 如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)、写出 点到 的三个顶点 的距离关系.(2)、如果点 分别在线段 上移动,移动中保持 ,请写出 的形状,并证明你的结论.25. 如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动. (1)、试证明:AD∥BC.(2)、在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
(1)、试证明:AD∥BC.(2)、在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.