河北省晋州市2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-02-03 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中是分式的是（）

A、 $\frac{x}{2}$ B、 $3 y$ C、 $\frac{x}{x - 1}$ D、 $\frac{x}{2} + y$

查看试题解析
2. 如图，△ABC≌△EFD，则下列说法错误的是（）

A、 $F C = B D$ B、 $E F$ 平行且等于 $A B$ C、 $A C$ 平行且等于 $D E$ D、 $C D = E D$

查看试题解析
3. 下列约分正确的是（）

A、 $\frac{x^{6}}{x^{2}}$ =x³； B、 $\frac{x + y}{x + y} = 0$ ； C、 $\frac{x + y}{x^{2} + x y} = \frac{1}{x}$ ； D、 $\frac{2 x y^{2}}{4 x^{2} y} = \frac{1}{2}$

查看试题解析
4. 下列式子中，正确的是（）

A、 $\sqrt[3]{- 7}$ ＝－ $\sqrt[3]{7}$ B、 $\sqrt{36}$ ＝±6 C、－ $\sqrt{3.6}$ ＝－0.6 D、 $\sqrt{{(- 8)}^{2}}$ ＝－8

查看试题解析
5. 下列实数中是无理数的是（）

A、 $\sqrt{9}$ B、 $\frac{22}{7}$ C、 $π$ D、 $- 0.323$

查看试题解析
6. 若分式 $\frac{x^{2} - 4}{x + 2} + 2$ 的值为 $0$ ，则x的值为（）

A、 $\pm 2$ B、 $2$ C、 $- 2$ D、 $0$

查看试题解析
7. 计算 $(\frac{a}{b} - \frac{b}{a}) \div \frac{a + b}{a}$ 的结果为（）

A、 $\frac{a - b}{b}$ B、 $\frac{a + b}{b}$ C、 $\frac{a - b}{a}$ D、 $\frac{a + b}{a}$

查看试题解析
8. 如图，如果AD∥BC，AD=BC，AC与BD相交于O点，则图中的全等三角形一共有（）

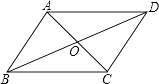A、3对 B、4对 C、5对 D、6对

查看试题解析
9. 在 $Δ A B C$ 和 $Δ A' B' C'$ 中， $A B = A' B'$ ， $∠ B = ∠ B'$ ，如果补充条件后，仍不一定能保证 $Δ A B C ≅ Δ A' B' C'$ ，则补充的这个条件是（）

A、 $A C = A' C'$ B、 $∠ A = ∠ A'$ C、 $B C = B' C'$ D、 $∠ C = ∠ C'$

查看试题解析
10. 如图，已知△ABC≌△CDE，其中AB＝CD，那么下列结论中，错误的是（）

A、AC＝CE B、∠BAC＝∠ECD C、∠ACB＝∠ECD D、∠B＝∠D

查看试题解析
11. 如图， $Δ A B D ≅ Δ E B C ， A B = 3 c m ， A C = 8 c m$ ，则 $D E$ 的长为（）

A、 $5 c m$ B、 $3 c m$ C、 $2 c m$ D、 $1 c m$

查看试题解析
12. 如图所示，在△ABC和△BDE中，点C在BD上，边AC交边BE于点F．若AC＝BD，AB＝ED，BC＝BE，则∠ACB等于（）

A、∠EDB B、∠BED C、 $\frac{1}{2}$ ∠AFB D、2∠ABF

查看试题解析
13. 关于x的方程 $\frac{3 x - 2}{x + 1} = 2 + \frac{m}{x + 1}$ 无解，则m的值为（）

A、﹣5 B、﹣8 C、﹣2 D、5

查看试题解析
14. 设 $A, B$ 均为实数，且 $A = \sqrt{m - 3}, B = \sqrt[3]{3 - m}$ ，则 $A, B$ 的大小关系是（）

A、 $A > B$ B、 $A = B$ C、 $A < B$ D、 $A \geq B$

查看试题解析
15. 一件工作，甲独做a小时完成，乙独做b小时完成，则甲，乙两人合作完成需要（）小时．

A、 $\frac{1}{a} + \frac{1}{b}$ B、 $\frac{1}{a b}$ C、 $\frac{1}{a + b}$ D、 $\frac{a b}{a + b}$

查看试题解析
16.
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点，根据图中标示的各点位置，与△ABC全等的是（　　）

A、△ACF B、△ACE C、△ABD D、△CEF

查看试题解析

二、填空题

17. -0.064的立方根是

查看试题解析
18. 三个全等三角形按如图的形式摆放，则 $∠ 1 + ∠ 2 + ∠ 3 =$ 度.

查看试题解析
19. 定义运算：a⊗b＝ $\frac{1}{a}$ + $\frac{1}{b}$ ，比如2⊗3＝ $\frac{1}{2}$ ＋ $\frac{1}{3}$ ＝ $\frac{5}{6}$ .下面给出了关于这种运算的几个结论：①2⊗（－3）＝ $\frac{1}{6}$ ；②此运算中的字母a，b均不能取零；③a⊗b＝b⊗a；④a⊗ （b＋c）＝a⊗b＋a⊗c.其中正确的是．（把所有正确结论都写在横线上）

查看试题解析
20. 如图，数轴上表示 $1$ 和 $\sqrt{2}$ 的对应点分别为 $A 、 B$ ，点 $B$ 是 $A C$ 的中点， $O$ 为原点．则线段长度： $A B =$ ， $A C =$ ， $O C =$

查看试题解析

三、解答题

21. 计算

(1)、计算： $(\frac{x}{x - 2} - \frac{x}{x + 2}) \div \frac{4 x}{x - 2}$

(2)、求 $x$ 的值： $81 x^{2} - 49 = 0$

查看试题解析
22. 如图，已知在 $Δ A B C$ 中， $C D$ 是 $A B$ 边上的高线， $B E$ 平分 $∠ A B C$ 交 $C D$ 于点 $E ， B C = 6 ， D E = 3$ ，求 $Δ B C E$ 的面积．

查看试题解析
23. 为顺利通过“国家文明城市”验收，某市政府拟对城区部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造，根据市政建设的需要，需在 $40$ 天内完成工程．现有甲、乙两个工程队有意承包这项工程，经调查知道，乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的 $2$ 倍，若甲、乙两工程队合作只需 $10$ 天完成．

(1)、甲、乙两个工程队单独完成此项工程各需多少天?

(2)、若甲工程队每天的工程费用是 $4.5$ 万元，乙工程队每天的工程费用是 $2.5$ 万元，请你设计一种方案（由单个工程队做或两个工程队合作），既能按时完工，又能使工程费用最少．

查看试题解析
24. 如图1，点 $M$ 为直线 $A B$ 上一动点， $△ A P B$ 、 $△ P M N$ 都是等边三角形，连接 $B N$

(1)、求证： $A M = B N$ ．

(2)、写出点 $M$ 在如图2所示位置时，线段 $A B$ 、 $B M$ 、 $B N$ 三者之间的数量关系．并证明．

查看试题解析