安徽省合肥市包河区2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-02-03 类型:期中考试
一、单选题
-
1. 下列四个点中,在第二象限的点是( ).A、(2,-3) B、(2,3) C、(-2,3) D、(-2,-3)2. 下列四个图形中,线段BE是△ABC的高的是( )A、
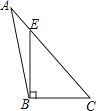 B、
B、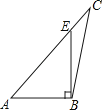 C、
C、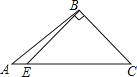 D、
D、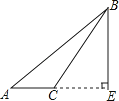 3. 在函数y= 中,自变量 的取值范围是( )A、 ≠0 B、 ≥-2 C、 >0 D、 ≥-2且 ≠04. 以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )A、1个 B、2个 C、3个 D、4个5. 将水匀速滴进如图所示的容器时,能符合题意反映容器中水的高度(h)与时间(t)之间对应关系的图象大致是( )
3. 在函数y= 中,自变量 的取值范围是( )A、 ≠0 B、 ≥-2 C、 >0 D、 ≥-2且 ≠04. 以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )A、1个 B、2个 C、3个 D、4个5. 将水匀速滴进如图所示的容器时,能符合题意反映容器中水的高度(h)与时间(t)之间对应关系的图象大致是( ) A、
A、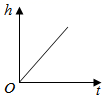 B、
B、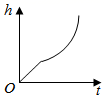 C、
C、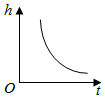 D、
D、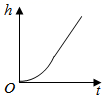 6. 若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )A、
6. 若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )A、 B、
B、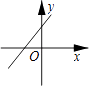 C、
C、 D、
D、 7. 如图,已知两直线l1:y= x和l2:y=kx﹣5相交于点A(m,3),则不等式 x≥kx﹣5的解集为( )
7. 如图,已知两直线l1:y= x和l2:y=kx﹣5相交于点A(m,3),则不等式 x≥kx﹣5的解集为( )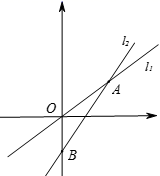 A、x≥6 B、x≤6 C、x≥3 D、x≤38. 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE度数为( ).
A、x≥6 B、x≤6 C、x≥3 D、x≤38. 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE度数为( ).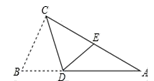 A、45°; B、64° ; C、71°; D、80°.9. 若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )A、-4<b<8 B、-4<b<0 C、b<-4或b>8 D、-4≤6≤810. A、B两地相距2400米,甲、乙两人从起点A地匀速步行去终点B地,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中正确的结论有( ):
A、45°; B、64° ; C、71°; D、80°.9. 若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )A、-4<b<8 B、-4<b<0 C、b<-4或b>8 D、-4≤6≤810. A、B两地相距2400米,甲、乙两人从起点A地匀速步行去终点B地,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中正确的结论有( ):①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若点A(a2-9,a+2)在y轴上,则a= .12. 已知y-2与x成正比,且当x=1时,y=-6,则y与x之间的函数关系式13. 已知方程组 的解为 ,则一次函数y=2x+3与y=ax+c的图象的交点坐标是 .14. 某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的关系:.15. 设0<a<1,关于x的一次函数y=ax+ (1-x),当1≤x≤2时的最大值是 . (用含a的代数式表示)16. 在某条街道上依次有图书馆、小明家、学校,某日小明从家出发先去学校,然后返回去图书馆,与此同时小亮从学校出发去图书馆,两人均匀速行走经过一段时间后两人同时到达图书馆.设两人步行的时间为x分,两人之间的距离为y米,y与x之间的函数关系如图所示,则学校与图书馆的距离是米.
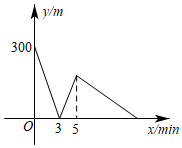
三、解答题
-
17. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-5, 1),B(4,0),C(2,5),将△ABC向右平移2个单位长度,再向下平移1个单位长度得到△EFG.
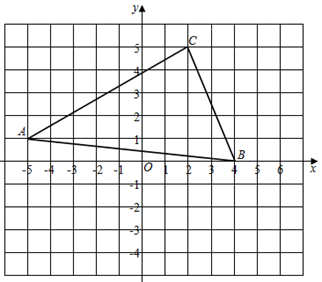 (1)、画出平移后的图形,并写出△EFG的三个顶点坐标.(2)、求△EFG的面积.18. 已知一个等腰三角形的周长是12cm,其中一边长是2cm,求另外两边的长.19. 根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)、画出平移后的图形,并写出△EFG的三个顶点坐标.(2)、求△EFG的面积.18. 已知一个等腰三角形的周长是12cm,其中一边长是2cm,求另外两边的长.19. 根据一次函数y=kx+b的图象,直接写出下列问题的答案: (1)、关于x的方程kx+b=0的解;(2)、当 时,代数式k+b的值;(3)、关于x的方程kx+b=-3的解.20. 已知函数y=(2m+1)x+m+2.(1)、若函数图象经过原点,求m的值;(2)、若该一次函数中y随着x的增大而减小,且它的图象与y轴的交点在x轴的上方,求整数m的值.21. 如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,求∠ADE和∠DAE的度数.
(1)、关于x的方程kx+b=0的解;(2)、当 时,代数式k+b的值;(3)、关于x的方程kx+b=-3的解.20. 已知函数y=(2m+1)x+m+2.(1)、若函数图象经过原点,求m的值;(2)、若该一次函数中y随着x的增大而减小,且它的图象与y轴的交点在x轴的上方,求整数m的值.21. 如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,求∠ADE和∠DAE的度数.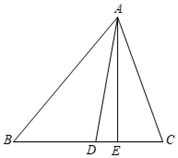 22. 随着新冠疫情的不断发展.某口罩生产企业从今年2月份开始增加生产N95口罩的流水线,生产N95口罩的总量y(万箱)与生产天数x(天)之间的关系如图所示,生产90天后,厂家改进了技术,平均每天的生产数量达到300箱.
22. 随着新冠疫情的不断发展.某口罩生产企业从今年2月份开始增加生产N95口罩的流水线,生产N95口罩的总量y(万箱)与生产天数x(天)之间的关系如图所示,生产90天后,厂家改进了技术,平均每天的生产数量达到300箱.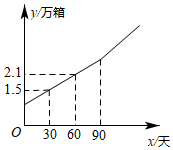 (1)、求y与x之间的函数表达式(2)、如果厂家制定总量不少于6万箱的生产计划,那么在改进技术后,至少还要多少天才能完成生产计划?23. 国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
(1)、求y与x之间的函数表达式(2)、如果厂家制定总量不少于6万箱的生产计划,那么在改进技术后,至少还要多少天才能完成生产计划?23. 国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:类别
彩电
冰箱
洗衣机
进价(元/台)
2000
1600
1000
售价(元/台)
2300
1800
1100
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)、商店至多可以购买冰箱多少台?(2)、购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?