安徽省安庆市2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-02-03 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各点中，在第二象限的是（）

A、 $(1 ， 0)$ B、 $(1 ， 1)$ C、 $(1 ， - 1)$ D、 $(- 1 ， 1)$

查看试题解析
2. 在平面直角坐标系中，第四象限内有一点 $M$ ，点 $M$ 到 $x$ 轴的距离为3，到 $y$ 轴的距离为2，则点 $M$ 的坐标是（）

A、 $(3 ， - 2)$ B、 $(2 ， - 3)$ C、 $(- 2 ， 3)$ D、 $(- 3 ， 2)$

查看试题解析
3. 下列命题中是真命题的是（　　）

A、同位角相等 B、平行于同一条直线的两条直线互相平行 C、互补的两个角是邻补角 D、如果一个数能被3整除，那么它一定能被6整除

查看试题解析
4. 下列图象中，表示y不是x的函数的是（）

A、 B、 C、 D、

查看试题解析
5. 在平面直角坐标系中，将点 $(3, 2)$ 向左平移1个单位长度，则所得的点的坐标是（）

A、 $(4, 2)$ B、 $(2, 2)$ C、 $(3, 3)$ D、 $(3, 1)$

查看试题解析
6. 如图， $F$ 是 $A B$ 上一点， $E$ 是 $A C$ 上一点， $B E$ 、 $C F$ 相交于点 $D$ ， $∠ A = 70 °$ ， $∠ A C F = 30 °$ ， $∠ A B E = 20 °$ ，则 $∠ B D C$ 的度数为（）

A、 $172 °$ B、 $80 °$ C、 $120 °$ D、 $60 °$

查看试题解析
7. 若一次函数 $y = (2 k - 1) x + k$ 的图象不经过第三象限，则 $k$ 的取值范围是（）

A、 $k > 0$ B、 $0 < k < \frac{1}{2}$ C、 $k \geq 0$ D、 $0 \leq k < \frac{1}{2}$

查看试题解析
8. 适合条件∠A＝ $\frac{1}{2}$ ∠B＝ $\frac{1}{3}$ ∠C的△ABC是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
9. 若等腰三角形中有两条边的长是2，5，则该三角形的周长是（）

A、9 B、12 C、9或12 D、无法确定

查看试题解析
10. 如图，动点 $P$ 在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点 $(1 ， 1)$ ，第2次接着运动到点 $(2 ， 0)$ ，第3次接着运动到点 $(3 ， 2)$ ，……按这样的运动规律，经过第2020次运动后，动点 $P$ 的坐标是（）

A、 $(2020 ， 0)$ B、 $(2020 ， 1)$ C、 $(2021 ， 1)$ D、 $(2021 ， 2)$

查看试题解析

二、填空题

11. 在 $△ A B C$ 中，若 $∠ A = 100 °$ ， $∠ B - ∠ C = 18 °$ ，则 $∠ C =$ ．

查看试题解析
12. 如果点 $P (m + 3, m + 1)$ 在坐标轴上，那么 $P$ 点坐标为．

查看试题解析
13. 对于平面坐标系中任意两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 定义一种新运算“ $*$ ”为： $(x_{1} ， y_{1}) * (x_{2} ， y_{2}) = (x_{1} y_{2} ， x_{2} y_{1})$ ．若 $A (x_{1} ， y_{1})$ 在第二象限， $B (x_{2} ， y_{2})$ 在第三象限，则 $A * B$ 在第象限．

查看试题解析
14.
甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中：
①甲队每天挖100米；
②乙队开挖两天后，每天挖50米；
③甲队比乙队提前3天完成任务；
④当x=2或6时，甲乙两队所挖管道长度都相差100米．
正确的有．（在横线上填写正确的序号）

查看试题解析

三、解答题

15. 已知 $y = (m - 2) x + | m | - 2$ ．

(1)、 $m$ 满足什么条件时， $y = (m - 2) x + | m | - 2$ 是一次函数？

(2)、 $m$ 满足什么条件时， $y = (m - 2) x + | m | - 2$ 是正比例函数？

查看试题解析
16. 已知点 $P (2 m + 4, m - 1)$ ，试分别根据下列条件，求出 $P$ 点的坐标．

(1)、点 $P$ 到 $x$ 轴的距离是5；

(2)、点 $P$ 在过点 $A (2, 3)$ 且与 $x$ 轴平行的直线上．

查看试题解析
17. 已知 $y$ 与 $x + 1$ 成正比例，且 $x = 2$ 时， $y = - 6$ ．

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、当 $y < 2$ 时，求 $x$ 的取值范围．

查看试题解析
18. 一次函数 $y = k x + b (k \neq 0)$ 满足，当 $- 1 \leq x_{1} \leq 2$ ， $- 2 \leq y_{1} \leq 1$ ，求这条直线的函数解析式．

查看试题解析
19. 快车与慢车分别从甲乙两地同时相向出发，匀速而行，快车到达乙地后停留 $0.5 h$ ，然后按原路原速返回，快车比慢车晚 $0.5 h$ 到达甲地．快慢两车距各自出发地的路程 $y (km)$ 与所用的时间 $x (h)$ 的关系如图所示．

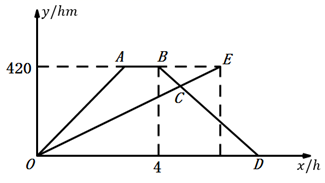(1)、甲乙两地之间的路程为 $km$ ；快车的速度为 $km/h$ ；慢车的速度为 $km/h$ ；

(2)、出发 $h$ ，快慢两车距各自出发地的路程相等；

(3)、快慢两车出发 $h$ 相距 $250 km$ ．

查看试题解析
20. 已知 $A D$ 、 $A E$ 分别是 $△ A B C$ 的高和角平分线．

(1)、如图所示，且 $∠ B = 77 °$ ， $∠ C = 32 °$ ，求 $∠ D A E$ ；

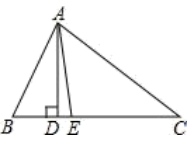(2)、若 $∠ B = α$ ， $∠ C = β (α > β)$ ，试用 $α$ ， $β$ 表示 $∠ D A E$ ；

(3)、若 $∠ B = α$ ， $∠ C = β (α < β)$ ，则 $∠ D A E =$ （直接填结果，无需说理）．

查看试题解析
21. 如图，直线 $l_{1}$ ： $y = x + 1$ 与直线 $l_{2}$ ： $y = - 2 x + n$ 相交于点 $P (1 ， b)$ ．

(1)、求点 $P$ 的坐标；

(2)、若 $y_{1} > y_{2} > 0$ ，求 $x$ 的取值范围；

(3)、点 $D (m ， 0)$ 为 $x$ 轴上的一个动点，过点 $D$ 作 $x$ 轴的垂线分别交 $l_{1}$ 和 $l_{2}$ 于点 $E$ ， $F$ ，当 $E F = 3$ 时，求 $m$ 的值．

查看试题解析
22. 已知：如图，点 $D$ 是 $△ A B C$ 内一点．

求证：

(1)、 $B D + C D < A B + A C$ ；

(2)、 $A D + B D + C D < A B + B C + A C$ ．

查看试题解析
23. 已知点 $A (- 3 ， - 2)$ ， $B (1 ， - 1)$ ， $C (0 ， - 4)$ ．

(1)、在平面直角坐标系 $x O y$ 中画出 $A$ ， $B$ ， $C$ 三点并求直线 $A B$ 的解析式；

(2)、求 $△ A B C$ 的面积；

(3)、已知一次函数 $y = a x + 3 a - 2$ （ $a$ 为常数）．
①求证：一次函数 $y = a x + 3 a - 2$ 的图象一定经过点 $A$ ；

②若一次函数 $y = a x + 3 a - 2$ 的图象与线段 $B C$ 有交点，直接写出 $a$ 的取值范围．

查看试题解析