天津市六校联考2016-2017学年高一上学期数学期中考试试卷

试卷更新日期：2017-10-19 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合A={0，1}，B={﹣1，0，a+3}，且A⊆B，则a等于（）

A、1 B、0 C、﹣2 D、﹣3

查看试题解析
2. 设全集U=R，A={x∈N|1≤x≤5}，B=x∈R|x²﹣x﹣2=0}，则图中阴影表示的集合为（）

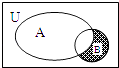A、{﹣1} B、{2} C、{3，4，5} D、{3，4}

查看试题解析
3. 函数f（x）= $\sqrt{4 - x}$ +lg（x﹣1）+（x﹣3）⁰ 的定义域为（）

A、{x|1＜x≤4} B、{x|1＜x≤4且x≠3} C、{x|1≤x≤4且x≠3} D、{x|x≥4}

查看试题解析
4. 已知a=log_0.60.5，b=ln0.5，c=0.6^0.5 ．则（）

A、a＞b＞c B、a＞c＞b C、c＞a＞b D、c＞b＞a

查看试题解析
5. 设函数f（x）=ln（1﹣x）﹣ln（1+x），则f（x）是（）

A、奇函数，且在（0，1）上是增函数 B、奇函数，且在（0，1）上是减函数 C、偶函数，且在（0，1）上是增函数 D、偶函数，且在（0，1）上是减函数

查看试题解析
6. 函数y=2^x^﹣¹+x﹣1的零点为x₀ ，则x₀∈（）

A、（﹣1，0） B、（0， $\frac{1}{2}$ ） C、（ $\frac{1}{2}$ ，1） D、（1， $\frac{3}{2}$ ）

查看试题解析
7. 已知f（x）=log $_{\frac{1}{2}}$ （x²﹣2x）的单调递增区间是（）

A、（1，+∞） B、（2，+∞） C、（﹣∞，0） D、（﹣∞，1）

查看试题解析
8. 已知函数f（x）= ${\begin{matrix} 3^{x} - 1 ， x > 0 \\ x^{2} + 1 ， x \leq 0 \end{matrix}$ ，若存在x₁∈（0，+∞），x₂∈（﹣∞，0]，使得f（x₁）=f（x₂），则x₁的最小值为（）

A、log₂3 B、log₃2 C、1 D、2

查看试题解析

二、填空题

9. 已知集合A={1，2^a}，B={a，b}，若A∩B={ $\frac{1}{4}$ }，则A∪B为．

查看试题解析
10. 设函数f（x）= ${\begin{matrix} 3 x - 5 ， x \geq 6 \\ f (x + 3) ， x < 6 \end{matrix}$ ，则f（2）= ．

查看试题解析
11. 已知定义域为[a﹣4，2a﹣2]的奇函数f（x）=2016x³﹣5x+b+2，则f（a）+f（b）的值为．

查看试题解析
12. 若幂函数 $y = (m^{2} - m - 1) x^{m^{2} - 2 m - 1}$ 在（0，+∞）上是增函数，则 m= ．

查看试题解析
13. 已知函数f（x）=log_ax+b（a＞0，a≠1）的定义域、值域都是[1，2]，则a+b= ．

查看试题解析
14. 已知函数f（x）是定义在R上的奇函数，若f（x）= ${\begin{matrix} l o g_{2} (x + 1) ， x \in [0 ， 1) \\ \frac{1}{2} x^{2} - 3 x + \frac{7}{2} ， x \in [1 ， + \infty) \end{matrix}$ ，则关于x的方程f（x）+a=0（0＜a＜1）的所有根之和为．

查看试题解析

三、三.解答题

15. 已知：函数f（x）= $\sqrt{4 - x}$ +lg（3^x﹣9）的定义域为A，集合B={x|x﹣a＜0，a∈R}，

(1)、求：集合A；

(2)、求：A∩B≠∅，求a的取值范围．

查看试题解析
16. 设集合A={x|（x﹣2m+1）（x﹣m+2）＜0}，B={x|1≤x+1≤4}．

(1)、若m=1，求A∩B；

(2)、若A∩B=A，求实数m的取值集合．

查看试题解析
17. 已知函数f（x）= $\frac{a}{x}$ +bx（其中a，b为常数）的图象经过（1，3）、（2，3）两点．
（I）求a，b的值，判断并证明函数f（x）的奇偶性；
（II）证明：函数f（x）在区间[ $\sqrt{2}$ ，+∞）上单调递增．

查看试题解析
18. 已知函数 f（x）= ${\begin{matrix} - x + 6 ， x \leq 2 \\ 3 + l o g_{a} x ， x > 2 \end{matrix}$ （a＞0且a≠1）

(1)、若a=2，解不等式f（x）≤5；

(2)、若函数f（x）的值域是[4，+∞），求实数a的取值范围．

查看试题解析
19. 已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若m，n∈[﹣1，1]，m+n≠0时，有 $\frac{f (m) + f (n)}{m + n}$ ＞0．
（Ⅰ）证明f（x）在[﹣1，1]上是增函数；
（Ⅱ）解不等式f（x²﹣1）+f（3﹣3x）＜0
（Ⅲ）若f（x）≤t²﹣2at+1对∀x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数t的取值范围．

查看试题解析