浙江省之江联盟2020届高三下学期数学4月开学考试试卷
试卷更新日期:2021-02-02 类型:开学考试
一、单选题
-
1. 集合 , ,则 ( )A、 B、 C、 D、2. 若函数 在区间 上存在零点,则常数a的取值范围为( )A、 B、 C、 D、3. “ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 已知实数 , 满足 则 的最小值为( )A、-3 B、 C、3 D、95. 函数f(x) 的图象大致是( )A、
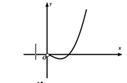 B、
B、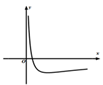 C、
C、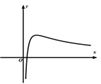 D、
D、 6. 已知 的内角 , , 的对边分别是 , , ,若 , , ,则 的面积为( )A、 B、 C、 D、7. 国际象棋比赛中规定,胜方得 分,负方得0分,和棋得0.5分.2019年浙江省青少年国际象棋公开赛中,某选手每场比赛得分的分布列如下:
6. 已知 的内角 , , 的对边分别是 , , ,若 , , ,则 的面积为( )A、 B、 C、 D、7. 国际象棋比赛中规定,胜方得 分,负方得0分,和棋得0.5分.2019年浙江省青少年国际象棋公开赛中,某选手每场比赛得分的分布列如下:1
0.5
0
且 ,则该选手进行一场比赛得分的期望一定不可能的是( )
A、0.3 B、0.5 C、0.7 D、0.88. 四面体 中, ,其余棱长均为4, , 分别为 , 上的点(不含端点),则( )A、不存在 ,使得 B、存在 ,使得 C、存在 ,使得 平面 D、存在 , ,使得平面 平面9. 已知动点 , 关于坐标原点 对称, , 过点 , 且与直线 相切.若存在定点 ,使得 为定值,则点 的坐标为( )A、 B、 C、 D、10. 数列 满足 ,且 ,则( )A、 , B、 , C、 , D、 ,二、填空题
-
11. 若复数 ( 为虚数单位),则复数 的虚部为; .12. 双曲线 的焦距是 , 离心率是 .13. 《九章算术》是我国古代内容极为丰富的数学名著,它系统地总结了战国、秦、汉时期的数学成就,书中将四个面都是直角三角形的三棱锥称之为“阳马”.若某“阳马”的三视图如图所示(单位: ),则该阳马的体积为 ,最长的棱长为 .
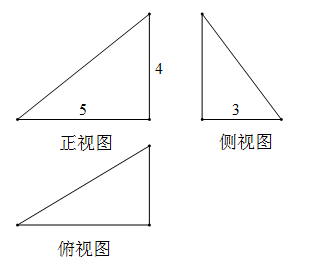 14. 若 ,则 , .15. “2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有种.16. 已知平面向量 满足 .对任意的 ,都有 成立,则 的取值范围是 .17. 已知函数 ( ,且 )在 上的最大值为 ,若 的最小值为 ,则常数 .
14. 若 ,则 , .15. “2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有种.16. 已知平面向量 满足 .对任意的 ,都有 成立,则 的取值范围是 .17. 已知函数 ( ,且 )在 上的最大值为 ,若 的最小值为 ,则常数 .三、解答题
-
18. 已知函数 .(1)、求函数 的单调递增区间;(2)、若 在区间 上有两个不同的解 , ,求 的范围及 的值.19. 如图,四棱锥 中, , , , , , .
 (1)、求证: ;(2)、求直线 与平面 所成角的正弦值.
(1)、求证: ;(2)、求直线 与平面 所成角的正弦值.
