辽宁省大连市名校联盟2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-02-02 类型：期中考试

进入出卷网下载

一、单选题

1. -3的相反数是（）。

A、3 B、 $\frac{1}{3}$ C、-3 D、 $- \frac{1}{3}$

查看试题解析
2. 2019 年“十一”黄金周期间，福鼎太姥山景区共接待游客约为 225000 人，这个数可用科学记数法表示为（）

A、 2.25×10⁴ B、22.5×10⁴ C、2.25×10⁵ D、0.225×10⁴

查看试题解析
3. 下列算式中，运算结果是负数的是（）

A、（-2）+7 B、5-（- 2） C、3´（-2） D、（-4）´（-2）

查看试题解析
4. 下列运算正确的是（）

A、2a²﹣a²＝1 B、5a²b﹣3ba²＝2a²b C、5a+a＝6a² D、3a+3b＝8ab

查看试题解析
5. 下列说法正确的是（）

A、单项式2 $x$ 的次数是0 B、单项式xy的系数是0 C、 $- 3$ 是单项式 D、 $- \frac{2}{3} a b$ 的系数是 $\frac{2}{3}$

查看试题解析
6. 方程 $2 x - 1 = 7 + x$ 的解是（）

A、 $x = 8$ B、 $x = 7$ C、 $x = 6$ D、 $x = \frac{8}{3}$

查看试题解析
7. 有理数a、b在数轴上的表示如图所示，那么（）

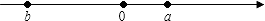A、﹣b＞a B、﹣a＜b C、b＞a D、|a|＞|b|

查看试题解析
8. 已知代数式 $x - 2 y$ 的值是-5，则代数式 $3 x - 6 y + 8$ 的值是（）

A、18 B、7 C、-7 D、-15

查看试题解析
9. 有甲、乙两桶油，从甲倒出19升到乙桶后，乙桶比甲桶还少6升，乙桶原有32升，则甲桶原来有油（）

A、36升 B、42升 C、60升 D、76升

查看试题解析
10. 若 $m \cdot n \neq 0$ ，则 $\frac{| m |}{m} + \frac{| n |}{n}$ 的值不可能是（）

A、0 B、1 C、2 D、-2

查看试题解析

二、填空题

11. 在1，-2，0，-1四个数中，最小的数是.

查看试题解析
12. 化简：2（a﹣1）﹣a，结果是.

查看试题解析
13. 若 $| x - 2 | + {(y + 3)}^{2} = 0$ ，则 $x - y =$ .

查看试题解析
14. 程大位是我国明朝商人，珠算发明家.他60岁时完成的《直指界法统宗》是东方古代数学名著.详述了传统的珠算规则，确立了算盘用法.书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁.意思是：有100个和尚分100个馒头，如果大和尚1人分3个馒头，小和尚3人分1个馒头，正好分完，求大、小和尚各有多少人.设小和尚有 $x$ 人，则可列方程为.

查看试题解析
15. 有一列式子，按一定规律排列成 $- 2 a$ ， $4 a^{3}$ ， $- 8 a^{5}$ ， $16 a^{7}$ ， $- 32 a^{9}$ …，则第7个式子.

查看试题解析
16. 一艘轮船在静水中的速度为 $a$ 千米/小时，水流的速度为10千米/小时，轮船顺水航行3小时的航程与逆水航行2小时的航程相差千米（用含 $a$ 的式子表示）.

查看试题解析

三、解答题

17. 计算

(1)、 $(- \frac{1}{2} + \frac{4}{9} - \frac{1}{6}) \times (- 18)$ ；

(2)、 $- 2^{2} - {(- \frac{3}{2})}^{2} \times \frac{2}{9} - \frac{1}{2}$ .

查看试题解析
18. 解方程： $3 - x = 6 x - 2 (x + 1)$ .

查看试题解析
19. 先化简，再求值： $x^{2} y - 2 (x^{2} y - 4 y) + 2 (x^{2} y - y)$ ，其中 $x = - 1$ ， $y = \frac{1}{2}$ .

查看试题解析

20. “十一”黄金周期间，大连圣亚海洋世界在8天假期中每天游客人数变化如下表（正号表示人数比前一天多，负号表示比前一天少），9月30日的游客人数为4.2万人.

日期	1日	2日	3日	4日	5日	6日	7日	8日
人数变化单位：万人	+1.8	-0.6	+0.2	-0.7	-1.3	+0.5	-2.4	+1

(1)、10月4日的游客人数为万人；

(2)、8天中游客人数最多的一天比最少的一天多万人；

(3)、如果每万名游客带来的经济收入约为80万元，则圣亚海洋世界黄金周8天的游客总收入约为多少万元？

查看试题解析

21. 七年级一班计划购买数学练习册和语文练习册共26本，已知每本数学练习册40元.每本语文练习册15元，经预算，共需要740元.求七年级一班计划购买数学练习册和语文练习册各多少本？

查看试题解析
22. 已知有理数 $a$ 、 $b$ 、 $c$ 在数轴上的位置如图所示，且 $| a | = | b |$ .

(1)、 $a^{2020} - b^{2020}$ 的值为；

(2)、化简： $| a - b | - | c - a | + | c - b |$ .

查看试题解析
23. 用边长为0.5米的黑、白两种颜色的正方形瓷砖按如图所示的方式铺宽为1.5米的小路.

(1)、铺第5个图形用白色正方形瓷砖块，黑色正方形瓷砖块；

(2)、按照此方式铺下去，铺第 $n$ 个图形用白色正方形瓷砖块，用黑色正方形瓷砖块（用含 $n$ 的代数式表示）；

(3)、若黑色正方形瓷砖每块价格25元，白色正方形瓷砖每块价格30元，若按照此方式恰好铺满12.5米长的小路，求铺满该段小路所需瓷砖的总费用.

查看试题解析
24.

(1)、用“ $>$ ”或“ $<$ ”或“ $=$ ”填空：
$| - 2 | + | 3 |$ $| - 2 + 3 |$ ， $| 2 | + | 3 |$ $| 2 + 3 |$ ， $| - 2 | + | - 3 |$ $| - 2 - 3 |$ ， $| 0 | + | - 3 |$ $| 0 - 3 |$ ；归纳：若 $a$ 、 $b$ 异号时， $| a | + | b |$ $| a + b |$ ，若 $a$ 、 $b$ 同号或至少有一个为0时， $| a | + | b |$ $| a + b |$ ；

(2)、根据上题中得出的结论，若 $| m | + | n | = 6$ ， $| m + n | = 2$ ，求 $m$ 的值.

查看试题解析

25. 某市自2020年1月起，对宾馆、饭店用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：

	月用水量（立方米）	水价（元/立方米）
第一级	50立方米以下（含50立方米）的部分	4.6
第二级	50立方米—150立方米（含150立方米）的部分	6.5
第三级	150立方米以上的部分	8

(1)、受疫情影响，某饭店7月份用水量为20立方米，则该饭店7月份需交的水费为元；

(2)、某饭店8月份用水量为160立方米，则该饭店8月份应交的水费为多少元？

(3)、某饭店9月份交水费1120元，求该饭店9月份的用水量.

查看试题解析

26. 已知点 $A$ 、 $B$ 在数轴上，点 $A$ 对应的数是 $- 3$ ，点 $B$ 在点 $A$ 的右边，且距点 $A$ 4个单位长度.

(1)、点 $B$ 所对应的有理数是

(2)、点 $C$ 是数轴上一动点，点 $C$ 到点 $A$ 和点 $B$ 的距离和的最小值为

(3)、若点 $D$ 到点 $A$ 、 $B$ 的距离之和是6个单位长度.
①求点 $D$ 所对应的有理数是多少？

②如果点 $Q$ 从点 $B$ 出发，沿数轴正方向以每秒1个单位长度的速度运动，同时点 $P$ 从点 $D$ 出发以每秒3个单位长度的速度沿数轴正方向运动， $t$ 秒后 $P$ 、 $Q$ 两点相距4个单位长度，求 $t$ 的值.

查看试题解析