江苏省镇江市句容市2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-02-02 类型：期中考试

进入出卷网下载

一、填空题

1. 若某次数学考试标准成绩定为80分，规定高于标准记为正，小高同学的成绩记作：＋12分，则她的实际得分为分.

查看试题解析
2. ﹣2的倒数是．

查看试题解析
3. 太阳半径约为696000千米，数字696000用科学记数法表示为千米.

查看试题解析
4. 比较大小 $- \frac{3}{2}$ $- \frac{2}{3}$ （填“＜”或“＞”）.

查看试题解析
5. 单项式 $- \frac{2}{3} a^{3} b$ 的系数是.

查看试题解析
6. 若代数式 $- 2 x^{m} y^{2}$ 与 $2 x^{3} y^{n}$ 是同类项，则 $m n$ =.

查看试题解析
7. 已知多项式（3﹣b）x⁵+x^a+x﹣6是关于x的二次三项式，则a²﹣b²的值为.

查看试题解析
8. 在数轴上点A表示的数为-2，点B也在数轴上，且A、B两点之间的距离是2，则点B 表示的数是.

查看试题解析
9. 若a-2b=3，则9-2a+4b的值为．

查看试题解析
10. 若 $| x | = 2$ ， $| y | = 3$ ，且 $x + y < 0$ ，则 $x - y$ 值为.

查看试题解析
11. 一组数值转换器按照下面程序计算，如果输出的结果是118，则输入的正整数为.

查看试题解析
12. 将一根绳子对折一次后从中间剪一刀，绳子变成3段；对折两次后从中间剪一刀，绳子变成5段：将这根绳子对折n次后从中间剪一刀，绳子变成段.

查看试题解析

二、单选题

13. 在数0， $- \frac{11}{7}$ ， $\frac{π}{2}$ ， $0. \overset{•}{1} \overset{•}{3}$ ，3.1415，2.3%， $0.10010001 \dots$ （相邻两个1之间依次增加1个0）中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
14. 下列计算正确的是（）

A、 $3 m^{2} - 2 m^{2} = 1$ B、 $3 m^{2} + 2 m^{2} = 5 m^{4}$ C、 $3 m^{2} n - 3 m^{2} n = 0$ D、 $3 m + 2 n = 5 m n$

查看试题解析
15. 若关于 $a ， b$ 的多项式 $2 (a^{2} + a b - 5 b^{2}) - (a^{2} - m a b + 2 b^{2})$ 中不含有 $a b$ 项，则m的值是（）

A、2 B、 $-$ 2 C、 $-$ 1 D、1

查看试题解析
16. 下列说法中正确的是（）

A、如果两个数的绝对值相等，那么这两个数相等 B、有理数分为正数和负数 C、互为相反数的两个数的绝对值相等 D、最小的整数是0

查看试题解析
17. 如图，有理数 $a 、 b 、 c 、 d$ 在数轴上的对应点分别是 $A 、 B 、 C 、 D$ ，若 $b 、 d$ 互为相反数，则 $a + c$ （）

A、小于0 B、等于0 C、大于0 D、不确定

查看试题解析
18. 如图所示，一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分(如图)，则这串珠子被盒子遮住的部分(包括白色和黑色)共有（）颗.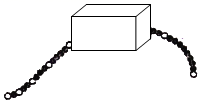

A、16 B、18 C、20 D、22

查看试题解析

三、解答题

19. 计算

(1)、 $24 - (- 16) + (- 25) - 32$

(2)、 $(- \frac{1}{2}) \times 2 \div 2 \times (- \frac{1}{2})$

(3)、 $- 2^{2} \times 5 - {(- 2)}^{3} \times \frac{1}{8} + 1$

(4)、 $(- \frac{1}{4} - \frac{5}{6} + \frac{8}{9}) \div {(- \frac{1}{6})}^{2} + {(- 2)}^{2} \times (- 6)$

查看试题解析
20. 化简：

(1)、 $2 （ 2 x - y) - (x + y)$

(2)、 $x^{2} y + [- 3 (2 x y - x^{2} y) - x y]$

查看试题解析
21. 先化简，再求值.
$(3 a^{2} b - a b^{2}) - \frac{1}{2} [a^{2} b - (2 a b^{2} - 4)] + 1$ ，其中a，b满足 ${(a + 2)}^{2} + | b - 1 | = 0$ .

查看试题解析
22. 有理数a、b、c，在数轴上的位置如图所示.

(1)、c0； $a + c$ 0；（用“＞、＜、=”填空）

(2)、化简： $| a + c | - | a - b | + | c |$

查看试题解析
23. 如图，大正方形的边长为a，小正方形的边长为b.

(1)、请你用含有a、b的式子表示阴影部分的面积；

(2)、当 $a = 7.3$ ， $b = 5$ 时，求阴影部分的面积.

查看试题解析

24. 定义☆运算：

观察下列运算：

（+3）☆（+15）＝ +18	（﹣14）☆（﹣7）＝ +21
（﹣2）☆（+14）＝﹣16	（+15）☆（﹣8）＝﹣23
0☆（﹣15）＝ +15	（+13）☆ 0＝ +13

(1)、请你认真思考上述运算，归纳☆运算的法则：

两数进行☆运算时，同号，异号.

特别地，0和任何数进行☆运算，或任何数和0进行☆运算，.

(2)、计算：（﹣11）☆ [0☆（﹣12）]＝.

(3)、若2×（﹣2☆a）﹣1＝8，求a的值.

查看试题解析

25. 某服装厂生产一种西装和领带，西装每套定价为200元，领带每条定价30元.厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的90％付款.
现某客户要到该服装厂购买西装20套，领带x条.(x＞20)

(1)、两种方案分别需要付款多少元?(用含x的代数式表示)

(2)、若x＝30，通过计算说明此时哪种方案购买较为合算.

查看试题解析
26. 已知 ${(x + 1)}^{6} = a x^{6} + b x^{5} + c x^{4} + d x^{3} + e x^{2} + f x + g$ .
当 $x = 1$ 时， ${(1 + 1)}^{6} = a \times 1^{6} + b \times 1^{5} + c \times 1^{4} + d \times 1^{3} + e \times 1^{2} + f \times 1 + g$

$∴ a + b + c + d + e + f + g = 2^{6} = 64$

这种给x取一个特殊数的方法叫赋值法.请你巧用赋值法，尝试解答下列问题.

(1)、当x为多少时，可求出g为多少？

(2)、求 $a - b + c - d + e - f + g$ 的值；

(3)、求 $a + c + e$ 的值.

查看试题解析
27. 我们知道：在数轴上，点M表示实数为a，点N表示实数为b，当 $a < b$ 时，点M、N之间的距离记作：MN = $b - a$ ；当 $a > b$ 时，点M、N之间的距离记作：MN = a-b，例如： $a = - 3 ， b = 2$ ，则MN = $2 - (- 3) = 5$ .
如图，点A、B、C是数轴上从左向右依次排列的三点，且 $A C = 15$ ， $B C = 9$ ，点B表示的数是-4.

(1)、点A表示的数是，点C表示的数是；

(2)、动点M、N分别从A、C同时出发，点M沿数轴向右运动，速度为1个单位长度∕秒，点N沿数轴向左运动，速度为2个单位长度∕秒，运动t秒后：
①点M表示的数，点N表示的数；(用含t的代数式表示)

②求当t为何值时，点M、N、B三点中相邻两个点之间的距离相等.(M、N、B三点中任意两点不重合)

查看试题解析