江苏省泰州市医药高新区2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-02-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、0 B、3.14 C、 $\frac{1}{3}$ D、π

查看试题解析
2. 下列各对数中，互为相反数的是（）

A、-（-3）与 $| - 3 |$ B、 $- \frac{1}{4}$ 与-0.25 C、-（+3）与+（-3） D、+（-0.1）与-（- $\frac{1}{10}$ ）

查看试题解析
3. 全校学生总人数是x人，其中女生人数占总人数的48%，则男生比女生多多少人（）

A、0.52x B、0.48x C、0.04x D、0.4x

查看试题解析
4. 若多项式3x^|m|+（m﹣2）x+1是关于x的二次三项式，则m的值（）

A、2或﹣2 B、2 C、﹣2 D、﹣4

查看试题解析
5. 关于x的方程x+a=6与方程2x-5=1的解相同，则常数a是（）

A、-3 B、3 C、2 D、-2

查看试题解析
6. 下列说法中①若m为任意有理数，则m²+0.1总是正数②绝对值等于本身的数是正数③若ab＞0，a+b＜0，则a＜0，b＜0④ $- x^{2} y$ 、0、 $\frac{m + n}{2}$ 、a都是单项式，错误的有（）个

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

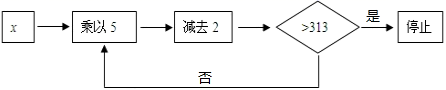
7. 向东走10m记作+10m，那么-7m表示.

查看试题解析
8. 一方有难，八方支援.2020年春节，“新冠”肺炎来袭，全国共计约42600名医护人员逆行援鄂，42600这个数据用科学记数法表示为.

查看试题解析
9. 比较大小： $- \frac{3}{4}$ $- \frac{4}{5}$

查看试题解析
10. 对有理数a，b定义运算 $*$ 如下： $a * b = \frac{a b}{1 - b}$ ，则（5 $*$ 2） $*$ 4=.

查看试题解析
11. 若 ${(x + 1)}^{2} + | 3 x - y | = 0$ ，则x²-2y=.

查看试题解析
12. 若 $- 2 x^{m} y^{4}$ 与 $3 x^{2} y^{n}$ 的和仍为单项式，则这两个单项式的和为.

查看试题解析
13. 当k=时，多项式 $x^{2} + k x y - 2 x y + 6$ 中不含xy项.

查看试题解析
14. 如果 $2 x^{2} - 3 x$ 的值为-1，则 $\frac{3}{2} x - x^{2} + 3$ 的值为.

查看试题解析
15. 输入x，按如图所示程序进行运算：规定：程序运行到“判断大于313”计为一次运算.若输入的x为8，则程序运算次停止.

查看试题解析
16. a、b、c、d为互不相等的有理数，且c=2，|a−c|=|b−c|=|d−b|=1，则a+b+c+d=.

查看试题解析

三、解答题

17. 计算：

(1)、 $(- 4) - (+ 13) + (- 5) - (- 9) + 7$

(2)、 ${(- \frac{2}{3})}^{2} \div \frac{9}{4} \times {(- 3)}^{3} - (- 2^{2} + \frac{5}{3}) \times {(- 1)}^{2020}$

查看试题解析
18. 解下列一元一次方程：

(1)、 $3 x - 2 = 10 - 2 (x + 1)$ ；

(2)、 $\frac{2 x + 1}{3} - \frac{5 x － 1}{6} = 1$

查看试题解析
19. 先化简再求值： $2 m - 3 n + [4 m - (3 m - n)]$ ，其中m=-1，n=2.

查看试题解析
20. 有理数a，b在数轴上的对应点如图所示：

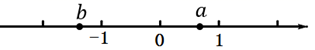(1)、填空：a-b0；b+10；2-a0；（填“＜”、“＞”或“=”）

(2)、化简： $| a - b | - | b + 1 | + | 2 - a |$ .

查看试题解析
21. 某天上午，一出租车司机始终在一条南北走向的笔直马路上营运.（出发点记作为点O，约定向南为正，向北为负）.期间一共运载6名乘客，行车里程(单位：千米)依先后次序记录如下：+7，-3，+6，-1，+2，-4.

(1)、出租车在行驶过程中，离出发点O最远的距离是千米；

(2)、将最后一名乘客送到目的地，出租车离出发点O多远？在O点的什么方向？

(3)、出租车收费标准为：起步价(不超过3千米)为10元，超过3千来的部分每千米的价格为1.6元，求司机这天上午的营业额.

查看试题解析
22. 已知A= $4 x^{2} - x + 1$ ，B= $5 x^{2} - x + 3$

(1)、求2A-3B；

(2)、试比较A、B的大小关系（写出比较过程）.

查看试题解析
23. 某同学解关于x的方程2（x+2）=a−3（x−2）时，由于粗心大意，误将等号右边的“−3（x−2）”看作“+3（x−2）”，其它解题过程均正确，从而解得方程的解为x=11，请求出a的值.

查看试题解析
24. 学校体育室有两个球筐，已知甲筐内的球比乙筐内球的个数的2倍还多6只.现进行如下操作：第一次，从甲筐中取出一半放入乙筐；第二次，又从甲筐中取出若干只球放入乙筐.设乙筐内原来有 $a$ 只球.

(1)、第一次操作后，乙筐内球的个数为只；（用含a的代数式表示）

(2)、若第一次操作后乙筐内球的个数比甲筐内球的个数多10只，求a的值；

(3)、第二次操作后，乙筐内球的个数可能是甲筐内球个数的2倍吗？请说明理由.

查看试题解析
25. 如图①是1个直角三角形和2个小正方形，直角三角形的三条边长分别是a、b、c，其中a、b是直角边.正方形的边长分别是a、b.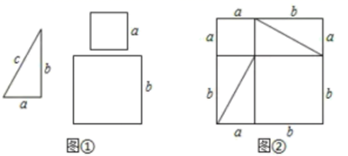

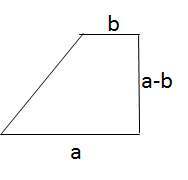
(1)、将4个完全一样的直角三角形和2个小正方形构成一个大正方形（如图②）.用两种不同的方法列代数式表示图②中的大正方形面积：方法一：；方法二：；

(2)、观察图②，试写出（a+b）² ， a² ， 2ab，b²这四个代数式之间的等量关系是：；

(3)、借助以上经验，利用以下两个完全一样的直角梯形，验证等式 $a^{2} - b^{2} = (a + b) (a - b)$ .请画出图形，并写出验证过程.

查看试题解析
26. 如图，多项式 $- 4 x^{2} y - 2 x y + 6$ 的三次项系数和常数项在数轴上分别对应A、B两点.点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动，当点P到达点B后立即返回，仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t（单位：秒）.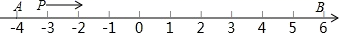

(1)、A、B两点表示的数分别是， .

(2)、在整个运动过程中，点P表示的有理数是多少？（用含t的代数式表示）.

(3)、当点P表示的有理数与原点距离3个单位时，直接写出所有满足条件的t的值.

查看试题解析