江苏省南通市如皋市2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 下列各数中,比 小5的数是( )A、-7 B、-3 C、3 D、72. 地球静止轨道卫星的静止轨道与地面的高度为35830千米.将35830用科学记数法表示应为( )A、 B、 C、 D、3. 计算 ,结果正确的是( )A、 B、 C、 D、4. 下列整式中,去括号后得 的是( )A、 B、 C、 D、5. 已知 与 是同类项,则 的值是( )A、2 B、3 C、4 D、56. 在有理数 , ,0, , , 中,负数的个数是( )A、1个 B、2个 C、3个 D、4个7. 若 , 互为倒数, , 互为相反数且 , 的绝对值等于 ,则 ( )A、3 B、-3 C、2 D、-58. 当 时,代数式 的值为 ,则当 时, 的值为( )A、2020 B、-2020 C、2018 D、-20189. 下面的四个说法:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,则 ,其中,正确的是( )A、①② B、①④ C、②③ D、③④10. 有两个正数 , ,且 ,把大于等于 且小于等于 的所有数记作 .例如,大于等于 且小于等于 的所有数记作 .若整数 在 内,整数 在 内,那么 的一切值中属于整数的个数为( )A、5个 B、4个 C、3个 D、2个
二、填空题
-
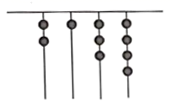
11. 地的海拔高度是 , 地的海拔高度是 , 地的海拔高度是 ,则 , , 三地中,地势最高的地方比地势最低的地方高 .12. 一次数学测试,如果 分为优秀,以 分为基准简记,例如 分记为 分,那么 分应记为分.13. 关于 , 的单项式 的次数为 ,则 的值为.14. 中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进 ,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是.
 15. 规定 ,如 ,据此可得 的值为.16. 如图,是一个运算程序的示意图,若开始输入的 的值为 ,则第 次输出的结果为.
15. 规定 ,如 ,据此可得 的值为.16. 如图,是一个运算程序的示意图,若开始输入的 的值为 ,则第 次输出的结果为.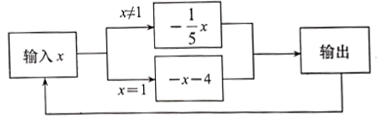 17. 如果整式 与整式 的和为一个数值 ,我们称 , 为数 的“友好整式”,例如: 和 是数 的“友好整式”; 和 为数 的“友好整式”.若关于 的整式 与 是数 的“友好整式”,则 的值为.18. 如图,把四张大小相同的长方形卡片(如图1)按图2、图3两种方式放在一个底面为长方形(长比宽多 )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图2中阴影部分的周长为 ,图3中阴影部分的周长为 ,那么 比 大 .
17. 如果整式 与整式 的和为一个数值 ,我们称 , 为数 的“友好整式”,例如: 和 是数 的“友好整式”; 和 为数 的“友好整式”.若关于 的整式 与 是数 的“友好整式”,则 的值为.18. 如图,把四张大小相同的长方形卡片(如图1)按图2、图3两种方式放在一个底面为长方形(长比宽多 )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图2中阴影部分的周长为 ,图3中阴影部分的周长为 ,那么 比 大 .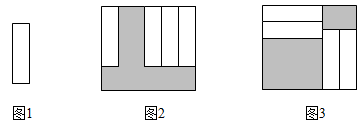
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 先化简,再求值:(1)、 ,其中 ;(2)、 ,其中 , .21. 已知 , ,解答下列各题:(1)、若 ,求 的值;(2)、若 ,求 的值.22. 有20袋大米,以每袋30千克为标准,超过的千克数用正数表述,不足的千克数用负数表述,具体称重记录如下:
与标准质量的差值(单位:千克)
-3
1
0
2.5
-2
-1.5
代数
1
2
3
8
4
2
(1)、20袋大米中,最重的一袋比最轻的一袋重千克;(2)、与标准重量比较, 袋大米总计超过多少千克或不足多少千克?(3)、若大米每千克售价3.5元,出售这20袋大米可卖多少元?23. 一名快递员骑电动车从饭店出发送外卖,向东走了2千米到达小红家,继续向东走了4千米到达小明家,然后又向西走了8千米到达小刚家,最后回到饭店.现以饭店为原点,以向东的方向为正方向,用一个单位长度表示 千米画数轴,并以点 , , , 分别表示饭店,小红家,小明家,小刚家.(1)、请画出数轴,并在数轴上标出点 , , , 的位置;(2)、小刚家距小红家多远?(3)、若小红步行到小明家每小时走 千米;小刚骑自行车到小明家每小时骑 千米,若两个人同时分别从自己家出发,问两个人能否同时到达小明家,若不能同时,谁先到达?24. 我们知道, ,类似地,我们也可以将 看成一个整体,则 .整体思想是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.请根据上面的提示和范例,解决下面的题目:
(1)、把 看成一个整体,求将 合并的结果;(2)、已知 ,求 的值;(3)、已知 , , 求 的值.25. 《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征.在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“纯数”.定义;对于自然数n,在计算n+(n+1)+(n+2)时,各数位都不产生进位,则称这个自然数n为“数”,例如:32是”纯数”,因为计算32+33+34时,各数位都不产生进位;23不是“纯数”,因为计算23+24+25时,个位产生了进位.(1)、判断2019和2020是否是“纯数”?请说明理由;(2)、求出不大于100的“纯数”的个数.26. 定义:对于数轴上的三点,若其中一个点与其它两个点的距离恰好满足 倍的数量关系,则称该点是其它两个点的“关联点”.例如,数轴上点 , , 所表示的数分别为 , , ,此时点 是点 , 的“关联点”.
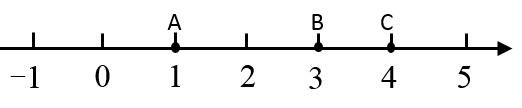 (1)、若点 表示数 ,点 表示的数 ,数 , , , 所对应的点分别 , , , ,其中是点 , 的“关联点”的是;(2)、点 表示数 ,点 表示的数 , 在为数轴上一个动点.
(1)、若点 表示数 ,点 表示的数 ,数 , , , 所对应的点分别 , , , ,其中是点 , 的“关联点”的是;(2)、点 表示数 ,点 表示的数 , 在为数轴上一个动点.①若点 在点 左侧,且点 是点 , 的“关联点”,则点 表示的数是;
②若点 在点 的右侧,点 , , 中,有一个点恰好是其它两个点的“关联点”,求出此时点 表示的数.