湖北省武汉市硚口区2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. -2020 的相反数是( )A、-2020 B、2020 C、 D、2. 单项式 的系数和次数分别是( )A、1,9 B、0,9 C、 ,9 D、 ,243. 2020年6月23日,我国成功发射北斗系统第55颗导航卫星,暨北斗三号最后一颗全球组网卫星,该卫星驻守在我们上方36000公里的天疆,数36000用科学记数法表示为( )A、 360×102 B、36×103 C、3.6×104 D、0.36×1054. 下列运算结果错误的是( )A、 B、 C、 D、5. 按括号内的要求用四舍五入法取近似数,其中正确的是( )A、 (精确到个位) B、 (精确到十分位) C、 (精确到0.1) D、 (精确到0.0001)6. 下列运算中正确的是( )A、 B、 C、 D、7. 已知 ,且 ,那么 等于( )A、8 B、-2 C、8或-2 D、-8或-28. 某药厂计划对售价为 元的药品进行降价销售,现在有三种方案.方案一:第一次降价10%,第二次降价30%;方案二;第一次降价20%,第二次降价15%﹔方案三:第一、二次降价均为20%三种方案哪种降价最多( )A、方案一 B、方案二 C、方案三 D、不能确定9. 如图,都是由棱长为1的正方体叠成的图形.例如:第①个图形由1个正方体叠成,第②个图形由4个正方体叠成,第③个图形由10个正方体叠成…,低此规律,第10个图形由 个正方体叠成,则 的值为( )
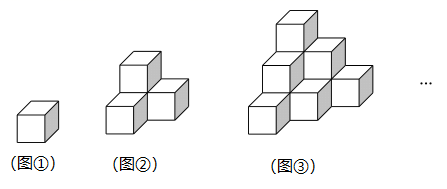 A、220 B、165 C、120 D、5510. 把两张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面为长方形(长为 ,宽为 )的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是( )
A、220 B、165 C、120 D、5510. 把两张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面为长方形(长为 ,宽为 )的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若零上8℃记作+8℃,则零下5℃记作℃.12. 在有理数中,绝对值最小的数是.13. 两船从同一个港口同时出发反向而行,甲船顺水航行了 小时,乙船逆水航行了 小时,两船在静水中的速度都是 ,水流速度是 则两船一共航行了 .(用含 的式子表示).14. 一个两位数M的个位上的数是 、十位上的数是 ,把这个两位数的十位上的数与个位上的数交换位置,所得的新数记为 ,则 .(用含 的式子表示)15. 如图,从左边第一个格子开始向右,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
5
4
则 , 第2019个格子填入的整数为
16. 如表被称为“杨辉三角”或“贾宪三角”.其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数: ,…,我们把第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第 个数记为 ,则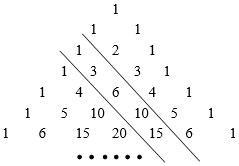
三、解答题
-
17. 计算(1)、(2)、(3)、(4)、18. 先化简,再求值(1)、 ,其中(2)、 ,其中19. 食品厂从生产的袋装食品中抽出样品 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
与标准质量的差值(单位:克)
-5
-2
0
1
3
6
袋数
1
4
3
4
5
3
(1)、这批样品的平均质量比标准质量是超过还是不足?平均每袋超过或不足多少克?(2)、若每袋标准质量为450克,求抽样检测的样品总质量是多少?20. 一辆货车从龙信广场出发负责送货,向西走了2千米到达光华小区,继续向西走了3.5千米到达实验初中,然后向东走了6.5千米到达商和广场,最后返回龙信广场. (1)、以龙信广场为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出光华小区、实验初中,商和广场的位置.(光华小区点 表示,实验初中用点 表示,商和广场用点 表示)(2)、光华小区与商和广场相距多远?(3)、若货车每千米耗油 升,那么这辆货车此次送货共耗油多少升?21. 已知 是有理数.(1)、当 时,先判断 的正、负符号,再求 的值;(2)、当 时,直接写出 的值.22. 一种笔记本的售价为2.2元/本,如果买100本以上,超过100本部分的售价为2元/本.(1)、小强和小明分别买了50本和200本,他们俩分别花了多少钱?(2)、如果小红买这种笔记本花了380元,她买了多少本?(3)、如果小红买这种笔记本花了n元,她又买了多少本?23. 如图是某年某月的月历,用如图所示的“凹”字型在月历中任意圈出5个数,设“凹“字型框中的五个数分别
(1)、以龙信广场为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出光华小区、实验初中,商和广场的位置.(光华小区点 表示,实验初中用点 表示,商和广场用点 表示)(2)、光华小区与商和广场相距多远?(3)、若货车每千米耗油 升,那么这辆货车此次送货共耗油多少升?21. 已知 是有理数.(1)、当 时,先判断 的正、负符号,再求 的值;(2)、当 时,直接写出 的值.22. 一种笔记本的售价为2.2元/本,如果买100本以上,超过100本部分的售价为2元/本.(1)、小强和小明分别买了50本和200本,他们俩分别花了多少钱?(2)、如果小红买这种笔记本花了380元,她买了多少本?(3)、如果小红买这种笔记本花了n元,她又买了多少本?23. 如图是某年某月的月历,用如图所示的“凹”字型在月历中任意圈出5个数,设“凹“字型框中的五个数分别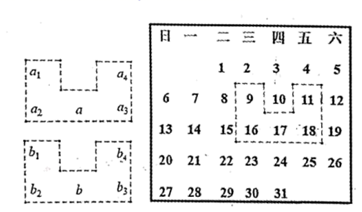 (1)、若 ,则 ,若 ,则 (用含 的式子表示);(2)、在移动“凹”字型框过程中,小胖说被框住的5个数字之和可能为106,大胖说被框住的5个数字之和可能为90,你同意他们的说法吗?请说明理由;(3)、若另一个“凹”字型框框住的五个数分别为 ,且 ,则符合条件的 的值为24. (问题背景)在数轴上,点 表示数 在原点 的左边,点 表示数 在原点 的右边,如图1所示,则有:① ;②线段 的长度
(1)、若 ,则 ,若 ,则 (用含 的式子表示);(2)、在移动“凹”字型框过程中,小胖说被框住的5个数字之和可能为106,大胖说被框住的5个数字之和可能为90,你同意他们的说法吗?请说明理由;(3)、若另一个“凹”字型框框住的五个数分别为 ,且 ,则符合条件的 的值为24. (问题背景)在数轴上,点 表示数 在原点 的左边,点 表示数 在原点 的右边,如图1所示,则有:① ;②线段 的长度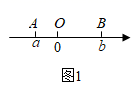 (1)、(问题解决)点 、点 ,点 在数轴上的位置如图2所示,三点对应数分别为
(1)、(问题解决)点 、点 ,点 在数轴上的位置如图2所示,三点对应数分别为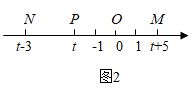
①线段 的长度为
②若点 为线段 的中点,则点 表示的数是(用含 的式子表示);
③化简
(2)、(关联运用)①已知:点 、点 、点 、点 在数轴上的位置如图3所示,点 对应数为 ,点 对应数为 ,若定长线段 沿数轴正方向以每秒 个单位长度匀速运动,经过原点 需要 秒,完全经过线段 需要 秒,求 的值;
②已知 ,当式子 取最小值时,相应的 的取值范围是 , 式子的最小值是.(用含 的式子表示)