浙江省温州市瑞安市西部联盟校(六校联盟)2021届九年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 某班有25名男生和20名女生,现随机抽签确定一名学生做代表参加学代会,则下列选项中说法正确的是( )A、男、女生做代表的可能性一样大 B、男生做代表的可能性较大 C、女生做代表的可能性较大 D、男、女生做代表的可能性的大小不能确定2. 已知 ,则 的值为( )A、 B、 C、 D、3. 如图所示,AD是 的直径,弦 ,若 ,则 等于( )
 A、 B、 C、 D、4. 在比例尺为 的地图上测得A、B两地间的图上距离为 ,则A、B两地间的实际距离为( )A、 B、 C、 D、5. 在学雷锋活动中,我校九(1)班有7位活动带头人,其中有4位是共青团员.现采用抽签的方式确定一位同学参加表彰大会,则被选中的同学为共青团员的概率是( )A、 B、 C、 D、6. 如图,将Rt ABC绕直角顶点C顺时针旋转90°,得到 A' B'C,连接AA',若∠1=20°,则∠B的度数是( )
A、 B、 C、 D、4. 在比例尺为 的地图上测得A、B两地间的图上距离为 ,则A、B两地间的实际距离为( )A、 B、 C、 D、5. 在学雷锋活动中,我校九(1)班有7位活动带头人,其中有4位是共青团员.现采用抽签的方式确定一位同学参加表彰大会,则被选中的同学为共青团员的概率是( )A、 B、 C、 D、6. 如图,将Rt ABC绕直角顶点C顺时针旋转90°,得到 A' B'C,连接AA',若∠1=20°,则∠B的度数是( )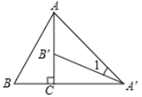 A、70° B、65° C、60° D、55°7. 如图,正六边形ABCDEF内接于 ,过点O作 弦BC于点M , 若 的半径为4,则弦心距OM的长为( )
A、70° B、65° C、60° D、55°7. 如图,正六边形ABCDEF内接于 ,过点O作 弦BC于点M , 若 的半径为4,则弦心距OM的长为( )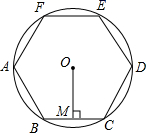 A、 B、 C、2 D、8. 抛物线 的图象如图所示.已知点 , , 三点都在该图象上,则 , , 的大小关系为( )
A、 B、 C、2 D、8. 抛物线 的图象如图所示.已知点 , , 三点都在该图象上,则 , , 的大小关系为( ) A、 B、 C、 D、9. 如图,正方形ABCD内接于 ,直径 ,则阴影部分的面积占圆面积的( )
A、 B、 C、 D、9. 如图,正方形ABCD内接于 ,直径 ,则阴影部分的面积占圆面积的( ) A、 B、 C、 D、10. 我校门口道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图1),图2是一个长为2米,宽为1米的矩形隔离栏,中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E , 点P)以及点A , 点B落上同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是( )
A、 B、 C、 D、10. 我校门口道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图1),图2是一个长为2米,宽为1米的矩形隔离栏,中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E , 点P)以及点A , 点B落上同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是( )
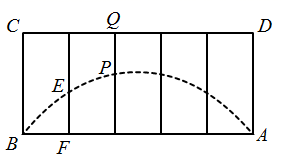 A、 米 B、 米 C、 米 D、 米
A、 米 B、 米 C、 米 D、 米二、填空题
-
11. 抛物线 的顶点坐标是12. 如图,直线 ,直线m , n分别与a , b , c相交于点A , B , C , D , E , F , 若 , , ,则 .
 13. 某烟花爆竹厂从5000件同类产品中随机抽取了100件进行质检,发现其中有3件不合格,估计该厂这5000件产品中不合格品约为件.14. 如图,点C , D是半圈O的三等分点,直径 .连结AC交半径OD于E , 则阴影部分的面积是 .
13. 某烟花爆竹厂从5000件同类产品中随机抽取了100件进行质检,发现其中有3件不合格,估计该厂这5000件产品中不合格品约为件.14. 如图,点C , D是半圈O的三等分点,直径 .连结AC交半径OD于E , 则阴影部分的面积是 . 15. 如图,在直角坐标系中,点A , C在x轴上,且 , , ,抛物线经过坐标原点O和点A , 若将点B向右平移5个单位后,恰好与抛物线的顶点D重合,则抛物线的解析式为 .
15. 如图,在直角坐标系中,点A , C在x轴上,且 , , ,抛物线经过坐标原点O和点A , 若将点B向右平移5个单位后,恰好与抛物线的顶点D重合,则抛物线的解析式为 . 16. 如图,抛物线 ( )交x轴于点A和点C(点A在点C左侧),交y轴于点B , 顶点为D , 且点D的纵坐标为 ,则 ;若点M是抛物线对称轴上一点,当 时,点M的坐标是 .
16. 如图,抛物线 ( )交x轴于点A和点C(点A在点C左侧),交y轴于点B , 顶点为D , 且点D的纵坐标为 ,则 ;若点M是抛物线对称轴上一点,当 时,点M的坐标是 .
三、解答题
-
17. 如图, 中,弦AB , CD相交于点E , 且 ,连结AC , BD , 求证: .
 18. 如图,已知二次函数 的图象经过 , 两点.
18. 如图,已知二次函数 的图象经过 , 两点. (1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.19. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .
(1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.19. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 . (1)、画出将绕点O顺时针旋转 后的图形,记为 ;(2)、在题(1)旋转过程中线段OA扫过的面积为(直接写出答案)20. 小明和小王在玩数学游戏,袋子中装有四张分别标上数字2,3,4,5的卡片(卡片除数字外其余都相同),先抽取一张卡片记录下所标数字,不放回再抽取一张.(1)、请你用画树状图或列表的方法列出所有可能结果.(2)、求两次抽到卡片上的数字之和是7的概率.(3)、双方约定规则:若两次抽到的数字之和为奇数,小明胜;若两数之和为偶数,则小王胜.该游戏规则对双方是否公平,请说明理由.21. 如图,抛物线 与x轴交于 和点 .
(1)、画出将绕点O顺时针旋转 后的图形,记为 ;(2)、在题(1)旋转过程中线段OA扫过的面积为(直接写出答案)20. 小明和小王在玩数学游戏,袋子中装有四张分别标上数字2,3,4,5的卡片(卡片除数字外其余都相同),先抽取一张卡片记录下所标数字,不放回再抽取一张.(1)、请你用画树状图或列表的方法列出所有可能结果.(2)、求两次抽到卡片上的数字之和是7的概率.(3)、双方约定规则:若两次抽到的数字之和为奇数,小明胜;若两数之和为偶数,则小王胜.该游戏规则对双方是否公平,请说明理由.21. 如图,抛物线 与x轴交于 和点 .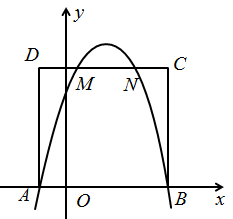 (1)、求该抛物线的表达式.(2)、以AB为边向上作矩形ABCD , 边CD与抛物线交于点M , N , 若 ,求矩形ABCD的周长.22. 如图,在 中, , (圆心 在 内部)经过B . C两点,交AC于点D , 交AB于点E,连结DE .
(1)、求该抛物线的表达式.(2)、以AB为边向上作矩形ABCD , 边CD与抛物线交于点M , N , 若 ,求矩形ABCD的周长.22. 如图,在 中, , (圆心 在 内部)经过B . C两点,交AC于点D , 交AB于点E,连结DE . (1)、求证: 是等腰直角三角形;(2)、若点D恰好是 的中点,且 ,求 的半径和 的长.23. 大润发超市购进一批成本价为20元 箱的陶山甘蔗,由往年销售经验可知,当销售单价为x元/箱( ),每天销售量为 箱,设超市销售该甘蔗每天获得的利润为W元.(1)、求W关于x的函数关系式.(2)、当销售单价x为多少元时,每天可获得最大利润?最大利润是多少?(3)、从今年11月份开始,物价部门建议甘蔗的利润不得高于成本的 ,求该超市每天获得的利润W的范围是多少?24. 如图,已知在矩形ABCD中, , ,点P是边CB上的一个动点,连接DP , 作 于点Q , 连结AQ , 作 的外接圆分别交线段CD , AB于点M , N , 连结AM , MQ .
(1)、求证: 是等腰直角三角形;(2)、若点D恰好是 的中点,且 ,求 的半径和 的长.23. 大润发超市购进一批成本价为20元 箱的陶山甘蔗,由往年销售经验可知,当销售单价为x元/箱( ),每天销售量为 箱,设超市销售该甘蔗每天获得的利润为W元.(1)、求W关于x的函数关系式.(2)、当销售单价x为多少元时,每天可获得最大利润?最大利润是多少?(3)、从今年11月份开始,物价部门建议甘蔗的利润不得高于成本的 ,求该超市每天获得的利润W的范围是多少?24. 如图,已知在矩形ABCD中, , ,点P是边CB上的一个动点,连接DP , 作 于点Q , 连结AQ , 作 的外接圆分别交线段CD , AB于点M , N , 连结AM , MQ . (1)、当 时,求 的度数.(2)、若 时,求证:点Q是 的中点.(3)、在点P的运动过程中,
(1)、当 时,求 的度数.(2)、若 时,求证:点Q是 的中点.(3)、在点P的运动过程中,①当 是等腰三角形时,求DM的长;
②当点P与点B重合时,连结QN , 记 的面积为 , 的面积为 , 的值为(直接写出答案).