浙江省宁波市北仑区七校精准教学联盟2021届九年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 如果 ,那么 ( )A、 B、 C、 D、2. 一个不透明的盒子中装有2个红球,1个白球和1个黄球,它们除颜色外都相同,若从中任意摸出一个球,则下列叙述正确的是( )A、摸到红球是必然事件 B、摸到黄球是不可能事件 C、摸到白球与摸到黄球的可能性相等 D、摸到红球比摸到黄球的可能性小3. 二次函数 的顶点坐标为( )A、 B、 C、 D、4. 若 ,则二次函数 的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 5. 若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )A、144° B、132° C、126° D、108°6. 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
5. 若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )A、144° B、132° C、126° D、108°6. 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( ) A、5 B、 C、3 D、7. 如图, 为 的直径, ,则 的度数为( )
A、5 B、 C、3 D、7. 如图, 为 的直径, ,则 的度数为( )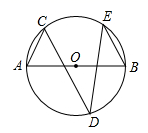 A、 B、 C、 D、8. 已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( )
A、 B、 C、 D、8. 已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( ) A、①②③ B、①②④ C、②③④ D、①③④9. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花,图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )
A、①②③ B、①②④ C、②③④ D、①③④9. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花,图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )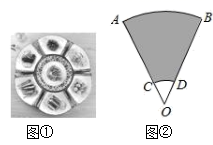 A、 B、 C、 D、10. 如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )
A、 B、 C、 D、10. 如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )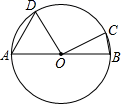 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一幅比例尺为 的地图上,某道路的长度为 ,则它的实际长度为 .12. 在一个不透明的口袋中,有大小、形状完全相同的红、绿两种颜色的球共15个,从中摸出红球的概率为 ,则袋中绿球的个数为个.13. 在二次函数中 ,y与x的部分对应值如下表:
x
......
-1
0
1
2
3
4
......
y
......
-7
-2
m
n
-2
-7
......
则m、n的大小关系为mn . (填“>”,“=”或“<”)
14. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度是.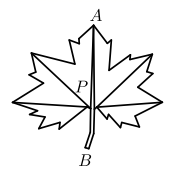 15. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是.
15. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是.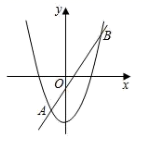 16. 如图,四边形 是 的内接四边形,对角线 , 交于点 ,且 ,若 ,则 等于 .
16. 如图,四边形 是 的内接四边形,对角线 , 交于点 ,且 ,若 ,则 等于 .
三、解答题
-
17.(1)、已知线段 是线段 、 的比例中项,如果 , ,求 的长度.(2)、已知 ,求 的值.18. 如图, 放置于平面直角坐标系中,按下面要求画图:
 (1)、画出 绕原点 逆时针旋转 的 .(2)、求点 在旋转过程中的路径长度.19. 小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏: , 是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形,同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请用画树状图或者列表的方式说明理由.
(1)、画出 绕原点 逆时针旋转 的 .(2)、求点 在旋转过程中的路径长度.19. 小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏: , 是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形,同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请用画树状图或者列表的方式说明理由.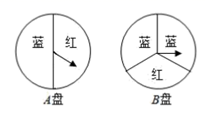 20. 如图,已知抛物线 与坐标轴交于 , , 三点,其中 , .
20. 如图,已知抛物线 与坐标轴交于 , , 三点,其中 , . (1)、求该抛物线的表达式;(2)、根据图象,写出 时, 的取值范围;(3)、平移该抛物线,使其顶点恰好落在原点,请写出一种平移方式及平移后的函数表达式.21. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .
(1)、求该抛物线的表达式;(2)、根据图象,写出 时, 的取值范围;(3)、平移该抛物线,使其顶点恰好落在原点,请写出一种平移方式及平移后的函数表达式.21. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .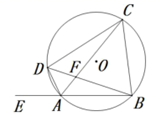 (1)、求证: 平分 ;(2)、若 ,求证: .22. 为确保贫困人口到2020年底如期脱贫,习总书记提出扶贫开发“贵在精准,重在精准,成败之举在于精准”,近年来扶贫工作小组对果农进行精准扶贫,帮助果农因地制宜种植一种有机生态水果并拓宽了市场,有机生态水果产量呈逐年上升,去年这种水果的产量是亩产约1000千克.(1)、预计明年这种水果产量要达到亩产1440千克,求这种水果亩产量去年到明年平均每年的增长率为多少?(2)、某水果店从果农处直接以每千克30元批发,专营这种水果.调查发现,若每千克的平均销售价为40元,则每天可售出200千克,若每千克的平均销售价每降低1元,每天可多卖出50千克,设水果店一天的利润为 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?23. 矩形 的一边长 ,且 ,以边 为直径的 交对角线 于 , ,如图,点 为下半圆上一点.
(1)、求证: 平分 ;(2)、若 ,求证: .22. 为确保贫困人口到2020年底如期脱贫,习总书记提出扶贫开发“贵在精准,重在精准,成败之举在于精准”,近年来扶贫工作小组对果农进行精准扶贫,帮助果农因地制宜种植一种有机生态水果并拓宽了市场,有机生态水果产量呈逐年上升,去年这种水果的产量是亩产约1000千克.(1)、预计明年这种水果产量要达到亩产1440千克,求这种水果亩产量去年到明年平均每年的增长率为多少?(2)、某水果店从果农处直接以每千克30元批发,专营这种水果.调查发现,若每千克的平均销售价为40元,则每天可售出200千克,若每千克的平均销售价每降低1元,每天可多卖出50千克,设水果店一天的利润为 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?23. 矩形 的一边长 ,且 ,以边 为直径的 交对角线 于 , ,如图,点 为下半圆上一点.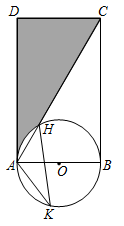 (1)、求 的度数;(2)、求 的长;(3)、求图中阴影部分的面积;(4)、若圆上到直线 距离等于3的点有且只有一个,请直接写出线段 的长.24. 如图, 点为 轴正半轴上一点, 交 轴于 、 两点,交 轴于 、 两点, 点为劣弧 上一个动点,连接 , ,且 , .
(1)、求 的度数;(2)、求 的长;(3)、求图中阴影部分的面积;(4)、若圆上到直线 距离等于3的点有且只有一个,请直接写出线段 的长.24. 如图, 点为 轴正半轴上一点, 交 轴于 、 两点,交 轴于 、 两点, 点为劣弧 上一个动点,连接 , ,且 , . (1)、如图1,求点 的坐标和 的度数;(2)、如图2,若 平分 交 于 点,当 点在运动时,线段 的长度是否发生变化;若不变求出其值,若发生变化,求出变化的范围;(3)、如图3,连接 ,当 点在运动时(不与 、 两点重合),求 的值.
(1)、如图1,求点 的坐标和 的度数;(2)、如图2,若 平分 交 于 点,当 点在运动时,线段 的长度是否发生变化;若不变求出其值,若发生变化,求出变化的范围;(3)、如图3,连接 ,当 点在运动时(不与 、 两点重合),求 的值.