江苏省南通市如皋市2021届九年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 抛物线 的顶点坐标为( )A、 B、 C、 D、2. 与点 在同一反比例函数图象上的点是( )A、 B、 C、 D、3. 一个圆锥的底面半径为 ,母线长为 ,这个圆锥的侧面积为( )A、 B、 C、 D、4. 将抛物线 平移得到抛物线 的步骤可以是( )A、向左平移4个单位,再向上平移1个单位 B、向左平移4个单位,再向下平移1个单位 C、向右平移4个单位,再向上平移1个单位 D、向右平移4个单位,再向下平移1个单位5. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
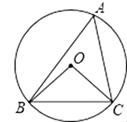 A、40° B、50° C、80° D、100°6. 如图,在平面直角坐标系中,函数 与 的图象交于点 ,则代数式 的值为( )
A、40° B、50° C、80° D、100°6. 如图,在平面直角坐标系中,函数 与 的图象交于点 ,则代数式 的值为( ) A、 B、 C、 D、7. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( )
A、 B、 C、 D、7. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( ) A、3 B、4 C、5 D、68. 如图,已知在平面直角坐标系中, 的顶点 , , ,函数 的图象经过点 ,则 的长为( )
A、3 B、4 C、5 D、68. 如图,已知在平面直角坐标系中, 的顶点 , , ,函数 的图象经过点 ,则 的长为( )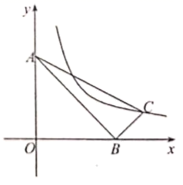 A、 B、 C、 D、9. 已知 , ,若抛物线 与线段 恰有两个交点,则 的取值范围为( )A、 B、 C、 D、10. 如图, 的顶点 是 上的一个动点, , ,边 , 分别交 于点 , ,分别过点 , 作 的切线交于点 ,且点 恰好在边 上,连接 ,若 的半径为 ,则 的最大值为( )
A、 B、 C、 D、9. 已知 , ,若抛物线 与线段 恰有两个交点,则 的取值范围为( )A、 B、 C、 D、10. 如图, 的顶点 是 上的一个动点, , ,边 , 分别交 于点 , ,分别过点 , 作 的切线交于点 ,且点 恰好在边 上,连接 ,若 的半径为 ,则 的最大值为( )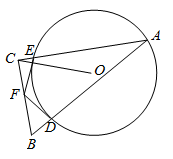 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,点P是反比例函数y= (x<0)图象上一点,PA垂直于y 轴,垂足为A,PB垂直于x轴,垂足为点B,若矩形 PBOA的面积为6,则k的值为.
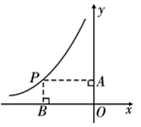 12. 如图, 是 的直径, 为 上的点,若 ,则 = .
12. 如图, 是 的直径, 为 上的点,若 ,则 = . 13. 过点 , , 的二次函数图象开口向(填“上”或“下”)14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .
13. 过点 , , 的二次函数图象开口向(填“上”或“下”)14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .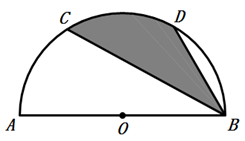 15. 二次函数 在3≤ ≤5范围内的最小值为.16. 据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形的外接一个圆,此圆外是一个同心圆”,如图所示.
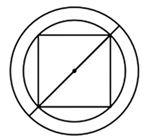
15. 二次函数 在3≤ ≤5范围内的最小值为.16. 据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形的外接一个圆,此圆外是一个同心圆”,如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为尺.(结果用最简根式表示)
 17. 调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
17. 调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).售价 (元/双)
200
240
250
400
销售量 (双)
30
25
24
15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为元.
18. 定义:在平面直角坐标系中,若点 满足横、纵坐标都为整数,则把点 叫做“整点”.如: 、 都是“整点”.抛物线 与 轴交于点 , 两点,若该抛物线在 、 之间的部分与线段 所围的区域(包括边界)恰有 个整点,则 的取值范围是.三、解答题
-
19. 如图, 的直径 和弦 相交于点 , , 的半径为 , ,求 的长.
 20. 如图,已知一次函数 的图象与反比例函数 的图象交于点 ,点 .
20. 如图,已知一次函数 的图象与反比例函数 的图象交于点 ,点 .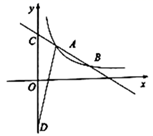 (1)、求反比例函数的表达式;(2)、若一次函数图象与y轴交于点C , 点D为点C关于原点O的对称点,求 的面积.21. 如图, 是 的弦, 交 于点 ,过点 的切线交 于点 .
(1)、求反比例函数的表达式;(2)、若一次函数图象与y轴交于点C , 点D为点C关于原点O的对称点,求 的面积.21. 如图, 是 的弦, 交 于点 ,过点 的切线交 于点 .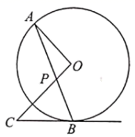 (1)、求证: 是等腰三角形;(2)、若 的半径为 , ,求 的长.22. 小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离B地的距离分别为 、 , 与x之间的数表达式 , 与x之间的函数表达式是 .(1)、小丽出发时,小明离A地的距离为 .(2)、小丽出发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?23.(1)、如图1,四边形 内接于 , .求证 .
(1)、求证: 是等腰三角形;(2)、若 的半径为 , ,求 的长.22. 小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离B地的距离分别为 、 , 与x之间的数表达式 , 与x之间的函数表达式是 .(1)、小丽出发时,小明离A地的距离为 .(2)、小丽出发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?23.(1)、如图1,四边形 内接于 , .求证 .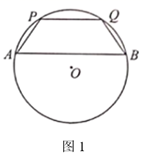 (2)、在 中, ,点 在以 为直径的半圆内,请你用无刻度的直尺分别按下列要求画图(保留画图痕迹),
(2)、在 中, ,点 在以 为直径的半圆内,请你用无刻度的直尺分别按下列要求画图(保留画图痕迹),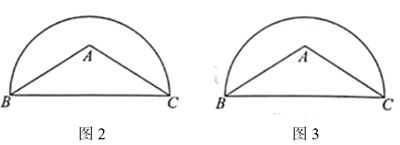
①在图2中,作弦 ,使 ;
②在图3中,以 为边作一个 的圆周角.
24. 定义: 叫做函数 的“反函数”.比如 就是 的“反函数”.数形结合是学习函数的一种重要方法,对于二次函数 ( 的常数),若点 在函数 的图象上,则点 也在其图象上,即从数的角度可以知道它的图象关于 轴对称.
根据上面的定义和提示,解答下列问题:
(1)、 的图象的对称轴是;(2)、①直接写出函数 的“反函数”的表达式为;②在如图所示的平面直角坐标系中画出 的“反函数”的大致图象;
(3)、若直线 与 轴交于点 ,与 轴交于点 ,与 的“反函数”图象交于 、 两点(点 的横坐标小于点 的横坐标),过点 作 轴,垂足为点 ,若 ,求 的值.25. 如图,直线 , 为垂足.以 圆心, 的半径作圆,交 于点 , ,交 于点 , .在 上任取一点 ,作 ,使 , ,顶点 , , 按顺时针方向分布,点 落在射线 上,且不在 内.若 的某一边所在直线与 相切,我们称该边为 的“相伴切边”.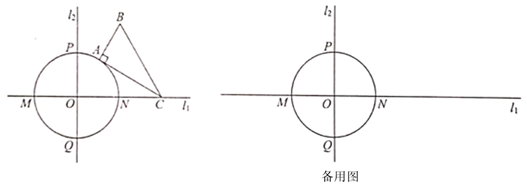 (1)、如图1, 为 的“相伴切边”, 平分 .求 的长;(2)、是否存在 三边中两边都是 的“相伴切边”的情形?若存在,请求出 的长;若不存在,请说明理由.26. 已知点 为二次函数 图象的顶点,直线 分别交 轴正半轴, 轴于点 , .
(1)、如图1, 为 的“相伴切边”, 平分 .求 的长;(2)、是否存在 三边中两边都是 的“相伴切边”的情形?若存在,请求出 的长;若不存在,请说明理由.26. 已知点 为二次函数 图象的顶点,直线 分别交 轴正半轴, 轴于点 , .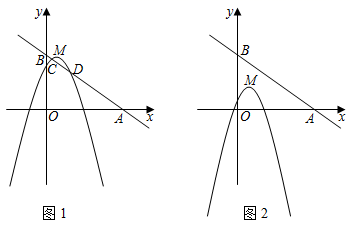 (1)、判断顶点 是否在直线 上,并说明理由.(2)、如图1,二次函数图象与直线相交于 , 两点,若 时, ,求 点的坐标;(3)、如图2,点 坐标为 ,点 在 内,若点 , 都在二次函数图象上,请直接写出 的取值范围,并结合 的取值范围确定 与 大小关系.
(1)、判断顶点 是否在直线 上,并说明理由.(2)、如图1,二次函数图象与直线相交于 , 两点,若 时, ,求 点的坐标;(3)、如图2,点 坐标为 ,点 在 内,若点 , 都在二次函数图象上,请直接写出 的取值范围,并结合 的取值范围确定 与 大小关系.