湖北省武汉市东湖新技术开发区2021届九年级上学期数学期中考试试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 方程 化成一般形式后,它的二次项系数和常数项分别是( )A、4,5 B、4,-5 C、4,81 D、4,-812. 下列汉字或字母中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 抛物线 的对称轴是( )A、 B、 C、 D、4. 不解方程,判断方程 的根的情况是( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、以上说法都不正确5. 抛物线 可由 如何平移得到( )A、先向右平移2个单位,再向下平移6个单位 B、先向右平移2个单位,再向上平移6个单位 C、先向左平移2个单位,再向下平移6个单位 D、先向左平移2个单位,再向上平移6个单位6. 已知点 与 关于原点对称,则 的值分别为( )A、 , B、 , C、 , D、 ,7. 某校九年级(1)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了1980张相片,如果全班有x名学生,根据题意,列出方程为( )A、 B、x(x+1)=1980 C、2x(x+1)=1980 D、x(x-1)=19808. 已第二次函数 图象上三点 、 、 ,则 , , 的大小关系为( )A、 B、 C、 D、9. 如图, 是圆 的直径, 是弦,四边形 是平行四边形, 与 相交于点 ,下列结论错误的是( )
3. 抛物线 的对称轴是( )A、 B、 C、 D、4. 不解方程,判断方程 的根的情况是( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、以上说法都不正确5. 抛物线 可由 如何平移得到( )A、先向右平移2个单位,再向下平移6个单位 B、先向右平移2个单位,再向上平移6个单位 C、先向左平移2个单位,再向下平移6个单位 D、先向左平移2个单位,再向上平移6个单位6. 已知点 与 关于原点对称,则 的值分别为( )A、 , B、 , C、 , D、 ,7. 某校九年级(1)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了1980张相片,如果全班有x名学生,根据题意,列出方程为( )A、 B、x(x+1)=1980 C、2x(x+1)=1980 D、x(x-1)=19808. 已第二次函数 图象上三点 、 、 ,则 , , 的大小关系为( )A、 B、 C、 D、9. 如图, 是圆 的直径, 是弦,四边形 是平行四边形, 与 相交于点 ,下列结论错误的是( )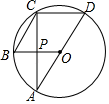 A、 B、 C、 D、 平分10. 已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )A、2个 B、3个 C、4个 D、5个
A、 B、 C、 D、 平分10. 已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 已知4是方程x2﹣c=0的一个根,则方程的另一个根是.12. 抛物线 的顶点坐标为.13. 要为一幅长 ,宽 的照片配一个相框,要求相框的四条边宽度相等,且相框所占面积为照片面积的四分之一,设相框边的宽度为 ,则可列出关于 的一元二次方程.14. 如图,将 绕顶点 逆时针旋转角度 得到 ,且点 刚好落在 上.若 , ,则 .
 15. 二次函数 ( 、 、 为常数, )中的 与 的部分对应值如下表:
15. 二次函数 ( 、 、 为常数, )中的 与 的部分对应值如下表:-1
0
3
3
3
当 时,下列结论中一定正确的是.(填序号即可)
① ;②若点 , 在该拋物线上,则 ;③ ;④对于任意实数 ,总有 .
16. 定义:有一组对角互余的四边形叫做对余四边形,如图,在对余四边形 中, , , , ,则线段 .
三、解答题
-
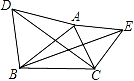
17. 解方程18. 是关于 的一元二次方程 的两个实数根,求代数式 , 的值.19. 如图,△ABD、△ACE都是等边三角形.求证:BE=DC.
 20. 如图,在 网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点, 均为格点,请按要求仅用一把无刻度的直尺作图.
20. 如图,在 网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点, 均为格点,请按要求仅用一把无刻度的直尺作图.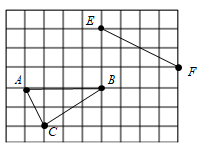 (1)、将 绕点 旋转 得到 ,请画出点 和 ;(2)、将格点线段 平移至格点线段 (点 的对应点分别为 ),使得 平分四边形 的面积,请画出线段 ;(3)、在线段 上找一点 ,使得 ,请画出点 .21. 如图, 的直径 为10,弦 为6, 是 的中点,弦 和 交于点 ,且 .
(1)、将 绕点 旋转 得到 ,请画出点 和 ;(2)、将格点线段 平移至格点线段 (点 的对应点分别为 ),使得 平分四边形 的面积,请画出线段 ;(3)、在线段 上找一点 ,使得 ,请画出点 .21. 如图, 的直径 为10,弦 为6, 是 的中点,弦 和 交于点 ,且 .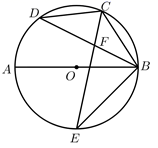 (1)、求证: ;(2)、求 的长.22. 网络销售已经成为一种热门的销售方式,某公司在某网络平台上进行直播销售板栗.已知板栗的成本价格为6元/ ,每日销售量 与销售单价 (元/ )满足一次函数关系,下表记录的是有关数据.经销售发现,销售单价不低于成本价且不高于30元/ .设公司销售板栗的日获利为 (元).
(1)、求证: ;(2)、求 的长.22. 网络销售已经成为一种热门的销售方式,某公司在某网络平台上进行直播销售板栗.已知板栗的成本价格为6元/ ,每日销售量 与销售单价 (元/ )满足一次函数关系,下表记录的是有关数据.经销售发现,销售单价不低于成本价且不高于30元/ .设公司销售板栗的日获利为 (元).(元/ )
7
8
9
4300
4200
4100
(1)、请求出日销售量 与销售单价 之间的函数关系式;(2)、当销售单价定为多少时,销售这种板栗日获利 最大?最大利润为多少元?(3)、当销售单价在什么范围内时,日获利 不低于42000元?23. 如图1, 中, , , 为 内一点,将 绕点 按逆时针方向旋转角 得到 ,点 的对应点分别为点 ,且 三点在同一直线上.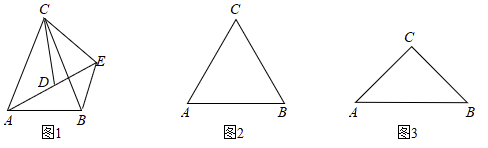 (1)、填空: (用含 的代数式表示);(2)、如图2,若 ,请补全图形,再过点 作 于点 ,然后探究线段 , , 之间的数量关系,并证明你的结论;(3)、如图3,若 , ,直接写出四边形 面积的最大值.24. 如图1,抛物线 : 经过点 ,顶点为 ,对称轴为直线 .
(1)、填空: (用含 的代数式表示);(2)、如图2,若 ,请补全图形,再过点 作 于点 ,然后探究线段 , , 之间的数量关系,并证明你的结论;(3)、如图3,若 , ,直接写出四边形 面积的最大值.24. 如图1,抛物线 : 经过点 ,顶点为 ,对称轴为直线 . (1)、求抛物线 的解析式;(2)、若点 为直线 上方的抛物线上的动点,当 面积最大时,求 点的坐标;(3)、如图2,将抛物线 向左平移至顶点在 轴上,平移后的抛物线 与 轴交于点 、 ,平行于 轴的直线 经过点 ,若点 为 轴上方的抛物线 上的动点,分别连接 、 ,并延长交直线 于 、 两点,若 、 两点的横坐标分别为 、 ,试探究 、 之间的数量关系.
(1)、求抛物线 的解析式;(2)、若点 为直线 上方的抛物线上的动点,当 面积最大时,求 点的坐标;(3)、如图2,将抛物线 向左平移至顶点在 轴上,平移后的抛物线 与 轴交于点 、 ,平行于 轴的直线 经过点 ,若点 为 轴上方的抛物线 上的动点,分别连接 、 ,并延长交直线 于 、 两点,若 、 两点的横坐标分别为 、 ,试探究 、 之间的数量关系.