浙江省温州市乐清市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-02 类型:期末考试
一、单选题
-
1. 由五个小立方体搭成的几何体如图所示,其主视图是
 A、
A、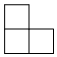 B、
B、 C、
C、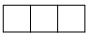 D、
D、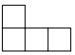 2. 一元一次不等式2(x﹣1)≥3x﹣3的解在数轴上表示为( )A、
2. 一元一次不等式2(x﹣1)≥3x﹣3的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 3. 某车间20名工人每天加工零件数如下表所示:
3. 某车间20名工人每天加工零件数如下表所示:每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
这些工人每天加工零件数的众数、中位数分别是( ).
A、5,5 B、5,6 C、6,6 D、6,54. 计算 的正确结果是( )A、 B、 C、 D、5. 如图,△ABC内接于⊙O,∠A=68°,则∠OBC等于( )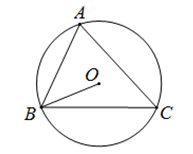 A、22° B、26° C、32° D、34°6. 从长度分别为2,4,6,8的四条线段中任选三条作边,能构成三角形的概率为( )A、 B、 C、 D、7. 已知点(-2, ),(1,0),(3, )都在二次函数 的图象上,则 ,0, 的大小关系是( )A、 B、 C、 D、8. 正方形网格中, 如图放置,则 的值为( )
A、22° B、26° C、32° D、34°6. 从长度分别为2,4,6,8的四条线段中任选三条作边,能构成三角形的概率为( )A、 B、 C、 D、7. 已知点(-2, ),(1,0),(3, )都在二次函数 的图象上,则 ,0, 的大小关系是( )A、 B、 C、 D、8. 正方形网格中, 如图放置,则 的值为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0).与y轴分别交于点B(0,4)与点C(0,16).则圆心M到坐标原点O的距离是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0).与y轴分别交于点B(0,4)与点C(0,16).则圆心M到坐标原点O的距离是( ) A、10; B、8 ; C、4 ; D、2 ;10. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A、10; B、8 ; C、4 ; D、2 ;10. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )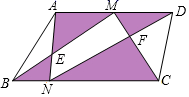 A、不变 B、一直变大 C、先减小后增大 D、先增大后减小
A、不变 B、一直变大 C、先减小后增大 D、先增大后减小二、填空题
-
11. 分解因式: .12. 若圆锥底面的半径为4,它的侧面展开图的面积为 ,则它的母线长为.13. 已知关于x的不等式组无解,则a的取值范围是14. 如图,宽为 的长方形图案由8个相同的小长方形拼成,若小长方形的边长为整数,则 的值为.
 15. 如图,直角坐标系中,A是反比例函数 图象上一点, B是y轴正半轴上一点,以OA,AB为邻边作 若点C及BC中点D都在反比例函数 ( , )图象上,则k的值为 .
15. 如图,直角坐标系中,A是反比例函数 图象上一点, B是y轴正半轴上一点,以OA,AB为邻边作 若点C及BC中点D都在反比例函数 ( , )图象上,则k的值为 . 16. 如图,矩形ABCD中,点E,F分别在边AD,CD上,且 , , 的外接圆⊙O恰好切BC于点G,BF交⊙O于点H,连结DH.若 ,则 .
16. 如图,矩形ABCD中,点E,F分别在边AD,CD上,且 , , 的外接圆⊙O恰好切BC于点G,BF交⊙O于点H,连结DH.若 ,则 .
三、解答题
-
17.(1)、计算: .(2)、先化简,再求值: ,其中 .18. 一个不透明的袋里装有2个红球,1个白球,1个黄球,它们除颜色外其余都相同.(1)、求从袋中摸出一个球是白球的概率;(2)、摸出1个球,记下颜色后不放回 , 搅拌均匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表).19. 如图都是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点.
 (1)、请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).(2)、如图1中所画的平行四边形的面积为.20. 如图,已知 , ,AC与BD交于O, .
(1)、请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).(2)、如图1中所画的平行四边形的面积为.20. 如图,已知 , ,AC与BD交于O, .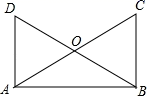
求证:
(1)、 ;(2)、 .21. 如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.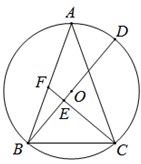 (1)、求证:∠BFC=∠ABC.
(1)、求证:∠BFC=∠ABC.
(2)、若⊙O的半径为5,CF=6,求AF长.
22. 某玩具批发市场A、B玩具的批发价分别为每件30元和50元,张阿姨花1200元购进A、B两种玩具若干件,并分别以每件35元与60元价格出售.设购入A玩具为x(件),B玩具为y(件).(1)、若张阿姨将玩具全部出售赚了220元,那么张阿姨共购进A、B型玩具各多少件?(2)、若要求购进A玩具的数量不得少于B玩具的数量,则怎样分配购进玩具A、B的数量并全部售出才能获得最大利润,此时最大利润为多少?(3)、为了增加玩具种类,张阿姨决定在1200元的基础上再增加投入,同时购进玩具A、B、C,已知玩具C批发价为每件25元,所购三种玩具全部售出,经核算,三种玩具的总利润相同,且A、C两种玩具的销量之和是玩具B销量的4.5倍,求玩具C每件的售价m元(直接写出m的值).23. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.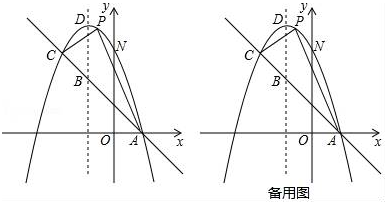 (1)、求抛物线及直线AC的函数关系式;(2)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;(3)、在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.24. 如图,矩形ABCD中, , ,动点E,F同时分别从点AB出发,分别沿着射线 AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动时间为t.
(1)、求抛物线及直线AC的函数关系式;(2)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;(3)、在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.24. 如图,矩形ABCD中, , ,动点E,F同时分别从点AB出发,分别沿着射线 AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动时间为t. (1)、 , (直接写出答案).(2)、当点E在线段AD上时,用关于t的代数式表示DE,DM.(3)、在整个运动过程中,
(1)、 , (直接写出答案).(2)、当点E在线段AD上时,用关于t的代数式表示DE,DM.(3)、在整个运动过程中,①连接CM,当t为何值时, 为等腰三角形;
②圆心O处在矩形ABCD内(包括边界)时,求t的取值范围直接写出答案.