广西北海市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-02-02 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，共36.0分）

1. sin45°的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 下列方程是关于x的一元一次方程的是（）

A、 $x + 1 = 0$ B、 $k^{2} x + 5 k + 6 = 0$ C、 $3 x^{2} + 2 x + \frac{1}{x} = 0$ D、 $(k^{2} x + 3) x^{2} + 2 x + 1 = 0$

查看试题解析
3. 如图，在△ABC中，∠C=90°，AB=3，BC=2，则cosB的值是（）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
4. 从鱼塘捕获同时放养的鲤鱼120条，从中任选8条称得每条鱼的质量分别是：1.3，1.7，1.5，1.4，1.4，1.2，1.7，1.0（单位：千克），那么估计这120条鱼的总质量约为（）

A、165千克 B、166千克 C、167千克 D、168千克

查看试题解析
5. 在用配方法解一元二次方程 $x^{2} - 6 x = 1$ 的过程中配方正确的是（）

A、 ${(x + 3)}^{2} = 8$ B、 ${(x - 3)}^{2} = 8$ C、 ${(x + 3)}^{2} = 1$ D、 ${(x - 3)}^{2} = 10$

查看试题解析
6. 如图，在 $△ A B C$ 中， $D E / / B C$ ，AD： $A B = 1$ ：3， $B C = 12$ ，则DE的长是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如果以 $12 m^{3} / h$ 的速度向水箱注水，5h可以注满.为了赶时间，现增加进水管，使进水速度达到 $Q (m^{3} / h)$ ，那么此时注满水箱所需要的时间 $t (h)$ 与 $Q (m^{3} / h)$ 之间的函数关系式为（）

A、 $t = \frac{60}{Q}$ B、 $t = 60 Q$ C、 $t = 12 - \frac{60}{Q}$ D、 $t = 12 + \frac{60}{Q}$

查看试题解析
8. 方程 $2 x^{2} - 5 x - 3 = 0$ 根的情况是（）

A、方程有两个不相等的实根 B、方程有两个相等的实根 C、方程没有实根 D、无法判断

查看试题解析
9. 学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO=4m，AB=1.6m，CO=1m，则栏杆C端应下降的垂直距离CD为（）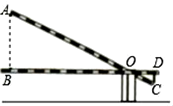

A、0.2m B、0.3m C、0.4m D、0.5m

查看试题解析
10. 为了庆祝教师节，市教育工会组织篮球比赛，赛制为单循环比赛（即每两个队比赛一场）共进行了45场比赛，则这次参加比赛的球队个数为（）

A、8 B、9 C、10 D、11

查看试题解析
11. 如图， $△ A B C$ 的三个顶点在边长为1的正方形网格的格点上，则 $tan (α + β)$ （） $t a n α + t a n β$ .

A、 $>$ B、 $<$ C、 $=$ D、 $\geq$

查看试题解析
12. 如图，点A在双曲线 $y = \frac{k}{x}$ 的第一象限的那一支上，AB垂直于y轴于点B，点C在x轴正半轴上，且 $O C = 2 A B$ ，点E在线段AC上，且 $A E = 3 E C$ ，点D为OB的中点，若 $△ A D E$ 的面积为18，则k的值为 $($ $)$

A、36 B、32 C、27 D、18

查看试题解析

二、填空题（本大题共6小题，共18.0分）

13. 一元二次方程 $x^{2} - 8 = 0$ 的解是 .

查看试题解析
14. 若 $\frac{b}{a} = \frac{7}{8}$ ，则 $\frac{a + b}{a - b} =$ .

查看试题解析
15. 为了估计池塘里有多少条鱼，从池塘里捕捞了1000条鱼做上标记，然后放回池塘里，经过一段时间，等有标记的鱼完全混合于鱼群中以后，再捕捞200条，若其中有标记的鱼有10条，则估计池塘里有鱼条．

查看试题解析
16. 计算： $\sqrt{2} s i n 45 ° + t a n 60 ° \cdot t a n 30 ° - c o s 60 ° =$ .

查看试题解析
17. 在平面直角坐标系中，点A的坐标为 $(m ， n)$ ，其中 $m \neq 0$ ，点B的坐标为 $(0 ， 5)$ ，若 $A B = 3$ ，记 $| \frac{n}{m} | = a$ ，则a的取值范围为.

查看试题解析
18. 已知点 $A (1, 2)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，则当 $x > 1$ 时，y的取值范围是.

查看试题解析

三、计算题（本大题共1小题，共6.0分）

19. 用公式法解一元二次方程： $x^{2} - 4 x + 2 = 0$ .

查看试题解析

四、解答题（本大题共7小题，共60.0分）

20. 如图，已知点O是坐标原点，B，C两点的坐标分别为 $(3 ， - 1)$ ， $(2 ， 1)$ .

(1)、以点O为位似中心在y轴的左侧将 $△ O B C$ 放大为原来的2倍 $($ 即新图形与原图形的相似比为 $2 ︰ 1)$ ，得到 $△ O B^{'} C^{'}$ ，画出图形；

(2)、分别写出B，C两点的对应点 $B^{'}$ ， $C^{'}$ 的坐标；

(3)、如果 $△ O B C$ 内部一点M的坐标为 $(x ， y)$ ，写出点M的对应点 $M^{'}$ 的坐标.

查看试题解析
21. 已知点 $A (2, 6)$ 、 $B (3, 4)$ 在某个反比例函数的图象上.

(1)、求此反比例函数的解析式；

(2)、若直线 $y = m x$ 与线段AB相交，求m的取值范围.

查看试题解析
22. 如图所示，一艘海轮位于灯塔P的北偏东 $65 °$ 的方向上，距离灯塔 $80 n m i l e$ 的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东 $34 °$ 方向上的B处.这时，B处距离灯塔P有多远？ $($ 结果取整数，参考数据： $cos 25 ° \approx 0.9063$ ， $sin 34 ° \approx 0.5592)$

查看试题解析
23. 校园安全问题已成为社会各界关注的热点问题，区教育局要求各学校加强对学生的安全教育，教育局安全科为了调查学生对“安全知识”内容的了解程度 $($ 程度分为：“A：十分熟悉”、“B：了解较多”、“C：了解较少、D：不了解” $)$ ，对我校中学部学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅不完整统计图，如图1，图2，请你根据图中提供的信息解答下列问题：

根据以上信息，解答下列问题

(1)、补全条形统计图；

(2)、本次抽样调查了名学生；在图1中扇形统计图中，求出“D”的部分所对应的圆心角等于度.

(3)、若我校中学部共有3100名学生，请你估计所有学生中，对“安全知识”内容的了解程度为“A：十分熟悉”和“B：了解较多”的学生共有多少名？

查看试题解析
24. 如图，一次函数 $y = x + m$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于A，B两点，且与x轴交于点C，点B的坐标为 $(- 1 ， - 2)$ .

(1)、求m及k的值；

(2)、连接OA，OB，求 $△ O A B$ 的面积；

(3)、结合图象直接写出不等式 $0 < x + m \leq \frac{k}{x}$ 组的解集.

查看试题解析
25. 随着正定旅游业的快速发展，外来游客对住宿的需求明显增大，某宾馆拥有的床位数不断增加.

(1)、该宾馆床位数从2016年底的200个增长到2018年底的288个，求该宾馆这两年 $($ 从2016年底到2018年底 $)$ 拥有的床位数的年平均增长率；

(2)、根据市场表现发现每床每日收费40元，288张床可全部租出，若每床每日收费提高10元，则租出床位减少20张.若想平均每天获利14880元，同时又减轻游客的经济负担每张床位应定价多少元？

查看试题解析
26. 如图，在 $△ A B C$ 中， $B A = B C = 20 c m$ ， $A C = 30 c m$ ，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒.

(1)、当x为何值时， $P Q / / B C$ ；

(2)、是否存在某一时刻，使 $△ A P Q$ ∽ $△ C Q B$ ？若存在，求出此时AP的长；若不存在，请说理由；

(3)、当 $C Q = 10$ 时，求 $\frac{S_{△ A P Q}}{S_{△ A B Q}}$ 的值.

查看试题解析