浙江省丽水市2021届九年级上学期数学期末考试试卷（B卷）
试卷更新日期：2021-02-02 类型：期末考试
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 下面四个手机应用图标中，属于中心对称图形的是（ ）A、
B、
C、
D、
2. 下列函数中，是二次函数的是（ ）A、y＝2x+1 B、y＝ C、y＝x2+2 D、y＝2x3. 如图，B为∠A一边上的任意一点，BC⊥AC于点C ， 那么tanA＝（ ）
A、 B、 C、 D、4. 某林业局将一种树苗移植成活的情况绘制成如统计图，由此可估计这种树苗移植成活的概率约为（ ）
A、0.95 B、0.90 C、0.85 D、0.805. 抛物线y=（x﹣1）2+2的顶点坐标是（ ）A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（1，2）6. 如图，在矩形ABCD中，AB＝6，AD＝8，若以点A为圆心，8为半径作⊙A ， 则下列各点在⊙A外的是（ ）
A、点A B、点B C、点C D、点D7. 如图，在△ABC中，∠AED＝∠B ， 若AB＝10，AE＝8，DE＝6，则BC的长为（ ）
A、 B、 C、 D、8. 如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是（ ）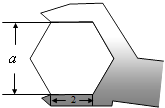
A、 cm B、 cm C、 cm D、1cm9. 关于x ， y的方程xy﹣x+y＝﹣3的整数解（x ， y）的对数为（ ）A、3 B、4 C、5 D、610. 如图，在△ABC中，∠ACB＝90°，∠B＝30°，D在AB上，E在CB上，A，C关于DE的对称点分别是G，F，若F在AB上，DG⊥AB，DG＝2，则DE的长是（ ）
A、3 ﹣3 B、3 ﹣ C、4 D、2二、填空题（本题有6小题，每小题4分，共24分）
-
11. 抛物线y＝x2+2与y轴的交点坐标为 ．12. 已知 ＝2，则 ＝ ．13. 用抽签的办法从甲，乙，丙，丁四位同学中，任选一位同学去打扫公共场地，选中甲同学的概率是 ．14. 如图，把两张宽度都是3cm的纸条交错的叠在一起，相交成角α．则重叠部分的面积为 ．
15. 已知直线y＝﹣x+1与双曲线y＝﹣ （x＞0）交于点M（m ， n），则代数式 + 的值是 ．16. 如图，在▱ABCD中，DE⊥BC ， AB＝ CE ， F是DE上一点，且∠BAF＝∠CDE ．
(1)、若CE＝2，则点B到AF的距离是；(2)、若DF＝2EF ， 则 的值为 ．三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）
-
17. 如图，已知正方形ABCD ， 用直尺和圆规作它的外接圆．
18. 如图，在Rt△BC中，∠C＝90°，AC＝2，AB＝3．
(1)、求BC的长；(2)、求sinA的值．19. 一个圆形人工湖示意图如图所示，弦AB是湖上的一座桥．已知AB长为100m ， 圆周角∠C＝45°，求这个人工湖半径OA的长．
20. 有A ， B ， C三种款式的帽子，E ， F两种款式的围巾，小赵任意选一顶帽子和一条围巾．(1)、用恰当的方法列举出所有可能选中的结果；(2)、求小赵恰好选中她所喜欢的B款帽子和F款围巾的概率．21. 如图，已知二次函数y＝﹣x2+bx+3的图象经过点（﹣2，3）．
(1)、求二次函数的表达式；(2)、给出一种平移方案，使该二次函数的图象平移后经过原点．22. 已知实数x ， y ， a ， b满足a﹣b＝x﹣y＝3，ax+by＝7．(1)、求ay+bx的值；(2)、求 的值．23. 已知关于x的二次三项式x2+（a+1）x+2﹣a ，(1)、若关于x的方程x2+（a+1）x+2﹣a＝0的两实数根为x1 ， x2 ， 且x12+x22＝2，求a的值；(2)、当a﹣6≤x≤5时，y＝x2+（a+1）x+2﹣a的图象与y＝x﹣1的图象只有一个交点，求a的取值范围．24. 如图，AB是⊙O的直径，点C在⊙O上，且AB＝2 ， ＝ ，D是⊙O上一动点，连结BD ， 过点B作BE⊥BD交直线DC于点E ．
(1)、当点D是 的中点时，求△BCD的面积；(2)、过点B作BF⊥DE于点F ， 求 的值；(3)、在点D运动过程中，求线段AE的最大值．