浙江省杭州市拱墅区锦绣育才教育集团2019-2020学年七年级下学期数学3月月考试卷

试卷更新日期：2021-02-02 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，∠1的同位角是（）

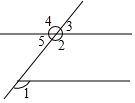A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
2. 已知二元一次方程组 ${\begin{cases} x + y = 1 \\ () \end{cases}$ 的解是 ${\begin{cases} x = - 2 \\ y = 3 \end{cases}$ ，则括号上的方程可能是（）

A、y﹣4x＝﹣5 B、2x﹣3y＝﹣13 C、y＝2x+5 D、x＝y﹣1

查看试题解析
3. 下列各式计算正确的是（）

A、（﹣6）⁵×6²＝﹣6⁷ B、x²+x²＝x⁴ C、（﹣a³）⁴＝a⁷ D、（﹣2a）⁴＝8a⁴

查看试题解析
4. 把一副三角板按如图所示摆放，使 $F D ∕ ∕ B C$ ，点 $E$ 恰好落在 $C B$ 的延长线上，则 $∠ B D E$ 的大小为（）

A、 $10 °$ B、 $15 °$ C、 $25 °$ D、 $30 °$

查看试题解析
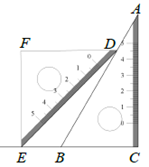5. 已知4^m＝x，8ⁿ＝y，其中m，n为正整数，则2^2m+6n＝（）

A、xy² B、x+y² C、x²y² D、x²+y²

查看试题解析
6. 若 $(x + a) (x + b)$ 的结果中不含 $x$ 的项，则 $a, b$ 满足（）

A、 $a = 0$ B、 $b = 0$ C、 $a = - b$ D、 $a = b$

查看试题解析
7. 若 ${(x + 2 y)}^{2} = {(x - 2 y)}^{2} + A$ ，则 $A$ 等于（）

A、 $8 x y$ B、 $- 8 x y$ C、 $8 y^{2}$ D、 $4 x y$

查看试题解析
8. 关于 $x,y$ 的方程组 ${\begin{matrix} a_{1} {x+b}_{1} {y=c}_{1} \\ a_{2} {x+b}_{2} {y=c}_{2} \end{matrix}$ 的解是 ${\begin{matrix} x = 4 \\ y = 1 \end{matrix}$ ，则关于 $x,y$ 的方程组 ${\begin{matrix} a_{1} (x-1) {+b}_{1} (-y) {=c}_{1} \\ a_{2} (x-1) {+b}_{2} (-y) {=c}_{2} \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$ B、 ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = 5 \\ y = 1 \end{matrix}$ D、 ${\begin{matrix} x = 5 \\ y = - 1 \end{matrix}$

查看试题解析
9. 小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小红看见了，说：“我也来试一试.”结果小红七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个洞，恰好是面积为4cm²的小正方形，则每个小长方形的面积为（）

A、135cm² B、108cm² C、68cm² D、60cm²

查看试题解析
10. 已知x₁ ， x₂ ， …，x₂₀₁₆均为正数，且满足M＝（x₁+x₂+…+x₂₀₁₅）（x₂+x₃+…+x₂₀₁₆），N＝（x₁+x₂+…+x₂₀₁₆）（x₂+x₃+…+x₂₀₁₅），则M，N的大小关系是（）

A、M＞N B、M＜N C、M＝N D、M≥N

查看试题解析

二、填空题

11. 如果把方程3x+y＝2写成用含x的代数式表示y的形式，那么y＝．

查看试题解析
12. 计算：（ $\frac{1}{2}$ x+y）（ $\frac{1}{2}$ x﹣y）＝.

查看试题解析
13. 如果 $x^{2} + 2 (m - 1) x + 25$ 是一个完全平方式，那么m的值为.

查看试题解析
14. 如图，已知 $A B / / C D / / E F$ ，则 $∠ 1 ， ∠ 2 ， ∠ 3$ 之间的数量关系是

查看试题解析
15. 如图，已知四边形纸片ABCD，其中∠B＝120°，∠D＝54°，现将其右下角向内折出△PC′R，恰使C′P∥AB，RC′∥AD，则∠C的度数是.

查看试题解析
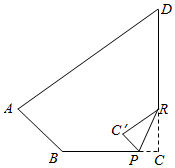16. 我们知道，很多数学知识相互之间都是有联系的．如图，图一是“杨辉三角”数阵，其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和；图二是二项和的乘方（a+b）ⁿ的展开式（按b的升幂排列）．经观察：图二中某个二项和的乘方的展开式中，各项的系数与图一中某行的数一一对应，且这种关系可一直对应下去．将（s+x）¹⁵的展开式按x的升幂排列得：（s+x）¹⁵＝a₀+a₁x+a₂x²+…+a₁₅x¹⁵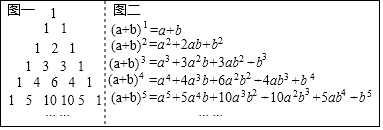

依上述规律，解决下列问题：（1）若s＝1，则a₂＝；（2）若s＝2，则a₀+a₁+a₂+…+a₁₅＝．

查看试题解析

三、解答题

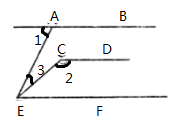
17. 计算或化简：

(1)、（﹣3x）³•（5x²y）

(2)、（ $\frac{1}{3} x - \frac{1}{4} x y$ ）•（﹣12y）

(3)、已知x²﹣2x﹣2＝0，将下式先化简，再求值：（x﹣1）²+（x+3）（x﹣3）+（x﹣3）（x﹣1）.

查看试题解析
18. 如图，已知∠C＝∠B，AB∥CD.

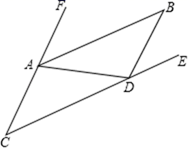(1)、试着先判断CF与BD所在的直线平行吗？请说明理由；

(2)、如果AB是∠FAD的平分线，且∠ADB＝98°，求∠B的度数.

查看试题解析
19. 若方程组 ${\begin{cases} 2 x - y = 7 \\ a x + y = b \end{cases}$ 和方程组 ${\begin{cases} x + b y = a \\ 3 x + y = 8 \end{cases}$ 有相同的解，求a，b的值.

查看试题解析
20. 如果一个正整数能表示为两个连续偶数的平方差，那么我们称这个正整数为“和谐数”，如：4＝2²﹣0² ， 12＝4²﹣2² ， 20＝6²﹣4² ，因此4，12，20这三个数都是“和谐数”.

(1)、36和2020这两个数是“和谐数”吗？为什么？

(2)、设两个连续偶数为2k+2和2k（其中取非负整数），由这两个连续偶数构成的“和谐数”是4的倍数吗？为什么？

查看试题解析

21. 一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	$5$	$8$	$10$
汽车运费（元/辆）	$400$	$500$	$600$

(1)、若全部物资都用甲、乙两种车型来运送，需运费

8200

元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知他们的总辆数为

16

辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

(3)、求出哪种方案的运费最省？最省是多少元？

查看试题解析

22. 当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式.例如，由图1，可得等式：（a+2b）（a+b）＝a²+3ab+2b².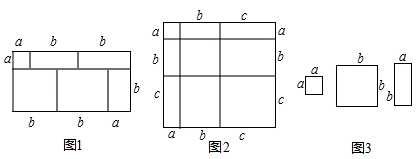

(1)、由图2，可得等式：.

(2)、利用（1）中所得到的结论，解决下面的问题：已知a+b+c＝12，ab+bc+ac＝47，求a²+b²+c²的值；

(3)、利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a²+5ab+2b²＝（2a+b）（a+2b）

查看试题解析
23. 钱塘江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况.如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a﹣3b|+（a+b﹣4）²＝0.假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN＝45°.

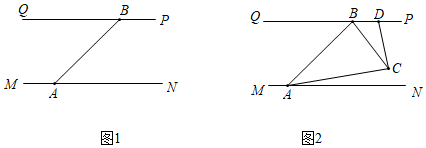(1)、求a、b的值；

(2)、若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图，两灯同时转动，在灯A射线到达AN之前，若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围.

查看试题解析