广东省深圳市盐田区2020-2021学年八年级上学期数学期末试卷
试卷更新日期：2021-02-02 类型：期末考试
一、选择题：本题共10小题，每小题3分，共30分．
-
1. -8的立方根是（ ）A、-2 B、2 C、±2 D、-42. 在平面直角坐标系中，点P (3，4)到原点的距离是（ ）A、3 B、4 C、5 D、73. 在AI计算机比赛预赛中，11名参赛者得分各不相同，按得分取前5名进入决赛。若佳佳知道自己的得分，要判断自己能否进入决赛，她只需知道11名参赛者得分的（ ）A、方差 B、平均数 C、众数 D、中位数4. 下列命题是真命题的为（ ）A、若两角的两边分别平行，则这两角相等 B、若两实数相等，则它们的绝对值相等 C、对应角相等的两个三角形是全等三角形 D、锐角三角形是等边三角形5. 如图，点E在射线AB上，要AD∥BC，只需（ ）
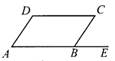A、∠A=∠CBE B、∠A=∠C C、∠C=∠CBE D、∠A+∠D= 180°6. 如图，数轴上点C所表示的数是（ ）
A、2 B、3.7 C、3.8 D、7. 若点A (x，5)与点B(2，y)关于y轴对称，则x+y的值是（ ）A、-7 B、-3 C、3 D、78. 把一根长7 m的钢管截成规格为2m和1 m的钢管(要求两种规格至少有一根)。在不造成浪费的情况下，不同的截法有（ ）A、1种 B、2种 C、3种 D、4种9. 如图，一次函数y=kx+b的图象经过点(-3，0)，则（ ）
A、b<0 B、方程kx+b=0 的解是x=-3 C、k<0 D、y随x的减小而增大10. 在△ABC中，AB=AC=5，BC=6，M是BC的中点，MN⊥AC于点N。则MN=（ ）A、 B、 C、6 D、11二、填空题：本题共5小题，每小题3分，共15分。
-
11. 登山队大本营所在地气温为5℃，海拔每升高1 km气温下降6℃。登山队员由大本营向上登高xkm时，所在位置的气温为y℃。则y与x的函数关系式是。12. 若 为整数，则正整数n的最小值是。13. 下图为甲、乙10次射击训练成绩的折线统计图。这些成绩的方差的大小关系是：S2甲S2乙。(选填“>”“=”“<”)
14. 与一次函数，y=2x-4图象平行的正比例函数图象经过第象限。15. 如图，∠AOB=30°，点M，N分别是射线OB，OA上的动点，点P为∠AOB内一点，OP=8。则△PMN的周长的最小值是。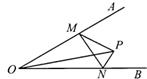
三、解答题：本题共7小题，共55分．解答应写出文字说明、证明过程或演算步骤．
-
16.(1)、计算：(2)、解方程：17. 为提高农民收入，村民自愿投资办起了养鸡场．办场时买来1000只小鸡，经过一段时间，饲养可以出售了。下表是这些鸡出售时质量的统计数据：
质量/ kg
1.0
1.2
1.5
1.8
2
频数
112
230
320
240
98
(1)、出售时这些鸡的平均质量是多少(结果保留小数点后一位) ？(2)、质量在哪个值的鸡最多？(3)、中间的质量是多少？18. 如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E。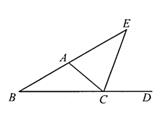
(1)、若∠B=30°，∠ACB=40°，求CE的度数；(2)、求证：∠BAC=∠B+2∠E。19. 根据市场调查，某厂某种消毒液的大瓶装(500g) 和小瓶装(250g) 两种产品的销售数量(按瓶计算)比为2：5。该厂每天生产这种消毒液22.5吨，这些消毒液应分装大、小瓶两种产品各多少瓶？20. 如图，在△ABC的三边上有D，E，F三点，点G在线段DF上，∠1与∠2互补，∠3=∠C。
(1)、若∠C=40°，求∠BFD的度数；(2)、判断DE与BC的位置关系，并说明理由。21. 一个有进水管与出水管的容器，从某时刻开始4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水，每分钟的进水量和出水量是两个常数。容器内水量y (单位：升)与时间x (单位：分钟)之间的关系如图所示。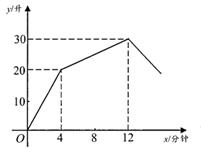
(1)、每分钟进水多少升？(2)、当4<x≤12时，求y关于x的函数解析式；(3)、容器中储水量不低于15 升的时长是多少分钟？22. 如图，直线AB：y1= x+m与x轴，y轴分别交于点A，B，直线CD：y2=-2x+8与x轴， y轴分别交于点C，D，直线AB，CD相交于点E，OD=2OA。(1)、写出点A的坐标和m的值；(2)、求S四边形OBEC；(3)、在坐标轴上是否存在点P，使得S△ABP= S△BDE？若存在，写出所有满足条件的点P的坐标：若不存在，说明理由。