广东省深圳市光明区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-02-02 类型:期末考试
一、选择题(共10小题,每小题3分,共30分。)
-
1. 下列各点在第二象限的是( )A、(- ,0) B、(-2,1) C、(0,-1) D、(2,-1)2. 若使算式3 ○ 的运算结果最小,则○表示的运算符号是( )A、+ B、- C、× D、÷3. 下列说法中,正确的是( )A、立方根等于本身的数只有0和1 B、1的平方根等于1的立方根 C、3< <4 D、面积为6的正方形的边长是4. 下列各图形中均有直线m∥n,则能使结论∠A=∠1-∠2成立的是( )A、
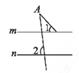 B、
B、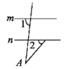 C、
C、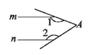 D、
D、 5. 解三元一次方程组 要使解法较为简便,首先应进行的变形为( )A、①+② B、①-② C、①+③ D、②-③6. 小明已求出了五个数据:6,4,3,4,□的平均数,在计算它们的方差时,出现了这一步:(3-5)2+(4-5)2+(4-5)2+(6-5)2+(□- 5)*=16(□是后来被遮挡的数据),则这组数据的众数和方差分别是( )A、4,5 B、4,3.2 C、6,5 D、4,167. 某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负一场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )A、 B、 C、 D、8. 如图,在Rt△ABC中,∠BCA=90° ,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )
5. 解三元一次方程组 要使解法较为简便,首先应进行的变形为( )A、①+② B、①-② C、①+③ D、②-③6. 小明已求出了五个数据:6,4,3,4,□的平均数,在计算它们的方差时,出现了这一步:(3-5)2+(4-5)2+(4-5)2+(6-5)2+(□- 5)*=16(□是后来被遮挡的数据),则这组数据的众数和方差分别是( )A、4,5 B、4,3.2 C、6,5 D、4,167. 某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负一场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )A、 B、 C、 D、8. 如图,在Rt△ABC中,∠BCA=90° ,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )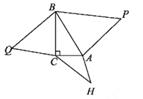 A、2 B、4 C、6 D、99. 如图,把一张纸片△ABC沿着DE对折,点C落在△ABC的外部点C'处,若∠1= 87°,∠2=17° ,则∠C的度数是( )
A、2 B、4 C、6 D、99. 如图,把一张纸片△ABC沿着DE对折,点C落在△ABC的外部点C'处,若∠1= 87°,∠2=17° ,则∠C的度数是( )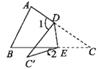 A、17° B、34° C、35° D、45°10. 如图,在平面直角坐标系中,点A(- 2,2),B(2,6),点P为x轴上一点,当PA+PB的值最小时,三角形PAB的面积为( )
A、17° B、34° C、35° D、45°10. 如图,在平面直角坐标系中,点A(- 2,2),B(2,6),点P为x轴上一点,当PA+PB的值最小时,三角形PAB的面积为( )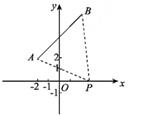 A、1 B、6 C、8 D、12
A、1 B、6 C、8 D、12二、填空题(共5小题,每小题3分,共15分)
-
11. 实数-64的立方根是。12. 有下列语句:①把无理数9表示在数轴上;②若a2>b2 , 则a>b;③无理数的相反数还是无理数。其中是真命题(填序号)。13. 已知一次函数y=-x+k的图象经过A(a,-1),B(b,-2)两点,则ab(填“>”“<"或“=”)。14. 如图,BD是正方形ABCD的对角线,点E在CD上,若CE=3,△ABE的面积为8,则△DBE的周长为。
 15. 如图,在平面直角坐标系中,点A,A1 , A2 , ……在工轴上,点P,P1 , P2 , 在直线l:y=kx+ (k>0)上,∠OPA=90°,点P(1,1) ,A(2,0),且AP1 , A1P2 , ……均与OP平行,A1P1 , A2P2 , ……均与AP平行,则有下列结论:①直线AP1的函数解析式为y=x-2;②点P2的纵坐标是 ;③点P2021的纵坐标为( )2021。其中正确的是(填序号)。
15. 如图,在平面直角坐标系中,点A,A1 , A2 , ……在工轴上,点P,P1 , P2 , 在直线l:y=kx+ (k>0)上,∠OPA=90°,点P(1,1) ,A(2,0),且AP1 , A1P2 , ……均与OP平行,A1P1 , A2P2 , ……均与AP平行,则有下列结论:①直线AP1的函数解析式为y=x-2;②点P2的纵坐标是 ;③点P2021的纵坐标为( )2021。其中正确的是(填序号)。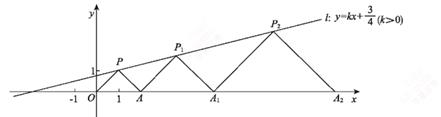
三、解答题(共7小题,共55分,其中第16题5分,第17题6分,第18~20题各8分,第21、22题各10分}
-
16. 解方程组:17.(1)、计算:(2)、已知 的小数部分是a, 的整数部分是b,求 -a的值。18. 某区举办中学生科普知识竞赛,各学校分别派出一支代表队参赛.知识竞赛满分为100分,规定85分及以上为“合格”,95分及以上为“优秀”。现将A,B两个代表队的竞赛成绩分布图及统计表展示如下:
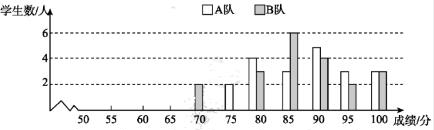
组别
平均分
中位数
方差
合格率
优秀率
A队
88
90
61
70%
30%
B队
a
b
71
75%
25%
(1)、求出成绩统计表中a,b的值。(2)、小明的成绩虽然在本队排名属中游,但是竞赛成绩低于本队的平均分,那么小明应属于哪个队?(3)、从平均分、合格率、优秀率、队内成绩的整齐性等方面进行综合评价,你认为集体奖应该颁给哪一队?19. 在正方形网格中建立如图所示的平面直角坐标系,格点(网格线交点)A(0,2),B(-2,-1)。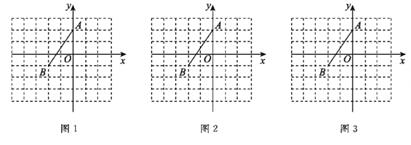 (1)、分别在图1、图2、图3中求作△ABC,并分别写出点C的坐标。
(1)、分别在图1、图2、图3中求作△ABC,并分别写出点C的坐标。①△ABC是轴对称图形,对称轴是y轴;
②△ABC是轴对称图形,对称轴是过点B且平行于坐标轴的直线;
③△ABC是轴对称图形,对称轴是过点B,但不平行于坐标轴的直线,且点C落在一、三象限以外的格点上。
(2)、在(1)③中作出的△ABC是三角形(按角分类),其面积为。20. 如图,已知∠CPB= 65°,AB∥CP,点D,E分别是PC,PB上一点,连接DE,使DE=PE,∠CDE的平分线与∠ABE的平分线交于点F。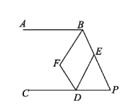 (1)、∠BED= ;(2)、求∠BFD的度数。21. 进入12月以来某些海鱼的价格逐渐上涨,某农贸市场水产商户老王只好在进货数量上做些调整。12月份前两周两种海鱼的价格情况如下表:
(1)、∠BED= ;(2)、求∠BFD的度数。21. 进入12月以来某些海鱼的价格逐渐上涨,某农贸市场水产商户老王只好在进货数量上做些调整。12月份前两周两种海鱼的价格情况如下表:鲅鱼价格
带鱼价格
第一周
8元/千克
18元/千克
第二周
10元/千克
20元/千克
(1)、老王第一周购进了一批鲅鱼和带鱼,总货款是1700元,若按第二周的价格购进与上周相同数量的鲅鱼和带鱼,则需多花300元,求老王第一周购进鲅鱼和带鱼分别是多少千克;(2)、若第二周将这两种鱼的进货总量减少到120千克,设购进鲅鱼a千克,需要支付的货款为w元,则w与a的函数关系式为;(3)、在(2)的条件下,若购进鲅鱼不超过80千克,则第二周老王购进这两种鱼的总货款最少应是多少元?22. 如图,点P(a,a+2)是平面直角坐标系xOy中的一个动点,直线l1:y=2x+5与x轴、y轴分别交于点A,B,直线l2经过点B和点(6,2)并与x轴交于点C。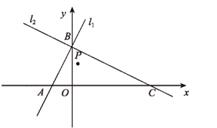 (1)、求直线l2的表达式及点C的坐标;(2)、点P会落在直线l2上吗?说明原因;(3)、当点P在△ABC内部时,求a的范围;(4)、若△OPC是以∠PCO为底角的等腰三角形,则下列各数:-8,-6,5,6,其中可以是点P的横坐标(写出所有符合要求的数)。
(1)、求直线l2的表达式及点C的坐标;(2)、点P会落在直线l2上吗?说明原因;(3)、当点P在△ABC内部时,求a的范围;(4)、若△OPC是以∠PCO为底角的等腰三角形,则下列各数:-8,-6,5,6,其中可以是点P的横坐标(写出所有符合要求的数)。