广东深圳坪山区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-02-02 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分。)
-
1. 在实数 、 、 、0中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 一次函数y= 2x+1的图象经过点( )A、(-1,-2) B、(-1,-1) C、(0,-1) D、(1,1)3. 下列各组线段中,不能构成直角三角形的是( )A、3,4,5 B、5,12, 13 C、8,15,17 D、6,7,94. 点P(-2,3)关于x轴对称的点的坐标为( )A、(2,-3) B、(-2, -3) C、(3,2) D、(2,3)5. 甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是9.1环,方差分别是S2甲=0.63,S2乙=20.58,S2丙=0.49,S2丁=0.46,则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁6. 若 , 是方程ax+by=6的两组解,则a,b的值为( )A、4,2 B、2,4 C、-4,-2 D、-2,-47. 下列四个命题中,真命题的是( )A、同角的补角相等 B、相等的角是对顶角 C、三角形的一个外角大于任何一个内角 D、两条直线被第三条直线所截,内错角相等8. 如图,已知a∥b,将一块含45°角的直角三角板(∠C=90° )按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
 A、80° B、70° C、85° D、75°9. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y和x的图象可能是( )A、
A、80° B、70° C、85° D、75°9. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y和x的图象可能是( )A、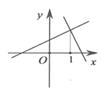 B、
B、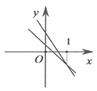 C、
C、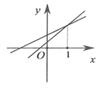 D、
D、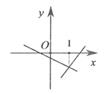 10. 如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为( )
10. 如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为( )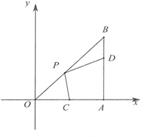 A、( , ) B、(2,2) C、( , ) D、( , )
A、( , ) B、(2,2) C、( , ) D、( , )二、填空题(本大题共5小题,每小题3分,共15分)
-
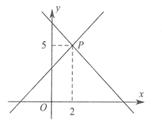
11. 的算术平方根是12. 如图,已知函数y=ax+ 3和y=bx+ 7的图象交于点P(2, 5),则关于x,y的方程组 的解是。
 13. 如图,在△ABC中,∠B=40°,∠BAC和∠ACB的平分线交于点D,则∠ADC的度数为 度。
13. 如图,在△ABC中,∠B=40°,∠BAC和∠ACB的平分线交于点D,则∠ADC的度数为 度。 14. 对于平面直角坐标系中的点P(x,y),若x,y满足|x-y|=1,则点P(x,y)就称为“好点”。例如:(5,6),因为|5-6|=1,所以(5, 6)是“好点”。已知一次函数y=3x+m(m为常数)图象上有一个“好点”的坐标是(3,4),则一次函数y=3x+ m(m为常数)图象上另一“好点”的坐标是。15. 如图,已知点A (4,6),B(0,3),一次函数y=3x + b图象经过点A,且与y轴相交于点C,若点P为线段AC上的一点,连接BP,将△ABP沿着直线BP翻折,使得点A的对应点恰好落在直线AB下方的y轴上,则点P的坐标为。
14. 对于平面直角坐标系中的点P(x,y),若x,y满足|x-y|=1,则点P(x,y)就称为“好点”。例如:(5,6),因为|5-6|=1,所以(5, 6)是“好点”。已知一次函数y=3x+m(m为常数)图象上有一个“好点”的坐标是(3,4),则一次函数y=3x+ m(m为常数)图象上另一“好点”的坐标是。15. 如图,已知点A (4,6),B(0,3),一次函数y=3x + b图象经过点A,且与y轴相交于点C,若点P为线段AC上的一点,连接BP,将△ABP沿着直线BP翻折,使得点A的对应点恰好落在直线AB下方的y轴上,则点P的坐标为。
三、解答题(本大题有七题,其中第16题4分、第17题8分、第18题7分、第19题8分、第20题8分、第21题10分、第22题10分,共55分)
-
16. 解方程组17. 计算:(1)、 ;(2)、18. 为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记录表》,绘制了如下不完整的体温统计表和扇形统计图。
班级学生体温统计表
组别
温度(℃)
人数
甲
36.3
6
乙
36.4
a
丙
36.5
20
丁
36.6
4
班级学生体温扇形统计图

请根据以上信息,解答下列问题:
(1)、统计表中a= , 该班学生体温的众数是 , 中位数是;(2)、扇形统计图中m= , 丁组对应的扇形的圆心角是度;(3)、求该班学生的平均体温(结果保留小数点后一位)。19. 已知:如图,点D,E,F,G都在△ABC的边上,DE∥AC,且∠1+∠2=180° (1)、求证:AD∥FG;(2)、若DE平分∠ADB,∠C=40°,求∠BFG的度数。20. “网约出行”改变了传统出行方式。某网约平台的打车出行计价规则为:打车总费用=里程费+耗时费,其中里程费按x元/公里计算,耗时费按y元/分钟计算.已知甲、乙两乘客用该平台网约打车出行,按其计价规则,其行驶里程数、平均车速及打车总费用等信息如下表:
(1)、求证:AD∥FG;(2)、若DE平分∠ADB,∠C=40°,求∠BFG的度数。20. “网约出行”改变了传统出行方式。某网约平台的打车出行计价规则为:打车总费用=里程费+耗时费,其中里程费按x元/公里计算,耗时费按y元/分钟计算.已知甲、乙两乘客用该平台网约打车出行,按其计价规则,其行驶里程数、平均车速及打车总费用等信息如下表:乘客
里程数(公里)
平均速度(公里/时)
打车总车费(元)
甲
8
60
20
乙
10
50
26
(1)、求x与y的值;(2)、小明的妈妈也采用了该平台的打车出行方式,其出行的平均车速为45公里1时,行驶了9公里,请你计算小明的妈妈应付车费多少元?21. 中国新冠肺炎疫情防控取得显著成效,为校园2021年防疫做物资储备,近日,某服装厂接到加工防护服任务,要求5天内加工完220套防护服,服装厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工-段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲乙两车间各自加工防护服数量y(套)与甲车间加工时间x (天)之间的关系如图1所示;未加工防护服w(套)与甲加工时间x (天)之间的关系如图2所示,请结合图象回答下列问题: (1)、甲车间每天加工防护服套,a=;(2)、求乙车间维修设备后,乙车间加工防护服数量y(套)与x(天)之间函数关系式;(3)、若55套服装恰好装满一辆货车,那么加工多长时间可装满第一辆货车?再加工多长时间恰好装满第二辆货车?22. 如图1,直线y=-x+b分别交x, y轴于A, B两点,点C(0,2),若S△ABC=2S△ACO。
(1)、甲车间每天加工防护服套,a=;(2)、求乙车间维修设备后,乙车间加工防护服数量y(套)与x(天)之间函数关系式;(3)、若55套服装恰好装满一辆货车,那么加工多长时间可装满第一辆货车?再加工多长时间恰好装满第二辆货车?22. 如图1,直线y=-x+b分别交x, y轴于A, B两点,点C(0,2),若S△ABC=2S△ACO。
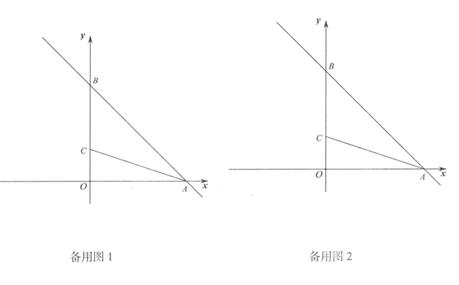 (1)、求b的值;(2)、若P是射线AB上的一点,S△PAC=2S△PCO , 求点P的坐标;(3)、如图2,过点C的直线交直线AB于E,已知D(-1,0),∠BEC=∠CDO,求直线CE的解析式。
(1)、求b的值;(2)、若P是射线AB上的一点,S△PAC=2S△PCO , 求点P的坐标;(3)、如图2,过点C的直线交直线AB于E,已知D(-1,0),∠BEC=∠CDO,求直线CE的解析式。