广东省深圳市南山区2020-2021学年九年级上学期数学期末试卷
试卷更新日期：2021-02-02 类型：期末考试
一、选择题(本题有10 小题，每小题3分，共30分．)。
-
1. 如图，这是由5个大小相同的正方体搭成的几何体，该几何体的左视图是（ ）
A、
B、
C、
D、
2. 下列命题是假命题的是（ ）A、四个角相等的四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直的平行四边形是菱形3. 在一个不透明的口袋中，装有若干个红球和3个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中红球的个数大约是（ ）A、20个 B、16个 C、15个 D、12个4. 一元二次方程x2+2x-1=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. △ABC与△A'B'C'是位似图形，且△ABC与△A'B'C'位似比是1：2，已知△ABC的面积是10，则△A'B'C'的面积是（ ）A、10 B、20 C、40 D、806. 关于反比例函数y= ，下列说法不正确的是（ ）A、函数图象分别位于第二、四象限 B、函数图象关于原点成中心对称 C、函数图象经过点(-6 ，-2 ) D、当x<0时，y随x的增大而增大7. 如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（ ）
A、 B、 C、 D、8. 如图，已知点A是反比例函数y= (x>0)的图象上一点，AB∥x轴交另一个反比例函数y= (x>0)的图象于点B，C为x轴上一点，若S△ABC=2，则k的值为（ ）
A、4 B、2 C、3 D、19. 如图，在菱形ABCD中，对角线AC、BD交于点O，且AC=6，BD=8，过A点作AE垂直BC，交BC于点E，则 的值为（ ）
A、 B、 C、 D、10. 如图，在矩形ABCD中，E是AD边的中点， BE⊥AC，垂足为点F，连接DF，下面四个结论：①CF=2AF ；②AD= CD；③DF=DC；④△AEF∽△CAB；⑤S四边形CDEF =S△ABF ， 其中正确的结论有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题(本题有5小题，每小题3分，共15分。)。
-
11. 已知 ，且a+b-2c=6，则a的值为 。12. 小王同学想利用树影测量校园内的树高．他在某一时刻测得小树高为1.5米时，其影长为1.2米，当他测量教学楼旁的一棵大树的影长时，因大树靠近教学楼，有一部分影子在墙上。经测量，地面部分影长为6.4米，墙上影长为1.4米，那么这棵大树高约为米。13. 设m、n是方程x2+x-1001=0的两个实数根，则m2+2m+n的值为。14. 如图，在矩形 中， 是边 的中点，连接 交对角线 于点 ，若 ， ，则 的长为 ．
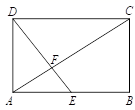15. 如图，在平面直角坐标系中，矩形ABCD的顶点A、D分别在x轴、y轴上，对角线BD∥x轴，反比例函数y= (k>0，x>0)的图象经过矩形对角线的交点E。若点A(2，0)、D(0，4)，则反比例函数的解析式为。
三、解答题：(16题6分，17题6分，18题7分，19题8分，20题9分，21题9分，22题10分，共计55分)
-
16. 解下列方程：(1)、2(x-2)2=x2-4(2)、2x2-4x-1=017. 甲、乙、丙、丁四位同学参加校田径运动会4X100米接力跑比赛，因为丁的速度最快，所以由他负责跑最后一棒，其他三位同学的跑步顺序随机安排。(1)、请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序；(2)、请求出正好由丙将接力棒交给丁的概率。18. 如图，在菱形ABCD中，E为对角线BD上一点，且AE=DE，连接CE。
(1)、求证：CE= DE。(2)、当BE=2，CE=1时，求菱形的边长。19. 某网店准备销售一种多功能旅行背包，计划从厂家以每个30元的价格进货，经过市场调查发现，当每个背包的售价为40元时，月均销量为280个，售价每增长2元，月均销量就相应减少20个。(1)、若使这种背包的月均销量不低于130个，每个背包售价应不高于多少元？(2)、在(1)的条件下，当该种书包销售单价为多少元时，销售利润是3120元？(3)、这种书包的销售利润有可能达到3700元吗？若能，请求出此时的销售单价；若不能，请说明理由。20. 如图，在平面直角坐标系中，直线y=3x+b经过点A(-1，0)，与y轴正半轴交于B点，与反比例函数y= (x>0)交于点C，且BC=2AB，BD∥x轴交反比例函数y= (x>0)于点D，连接AD。
(1)、b= ， k=；(2)、求△ABD的面积；(3)、若E为射线BC上一点，设E的横坐标为m，过点E作EF∥BD，交反比例函数y= (x>0)的图象于点F，且EF= BD，求m的值。21. 问题背景：如图1，在四边形ABCD中，∠B+∠D=180° ，AB=AD，∠BAD=a，以点A为顶点作一个角，角的两边分别交BC、CD于点E、F，且∠EAF= α，连接EF。试探究：线段BE、DF、EF之间的数量关系。
(1)、特殊情景在上述条件下，小明增加条件“当∠BAD=∠B=∠D= 90°时”如图(2)，小明很快就判断出线段BE、DF、EF之间的数量关系为：。
(2)、类比猜想类比特殊情景，小明猜想：在如图(1)的条件下线段BE、DF、EF之间的数量关系是否仍然成立？若成立，请你帮助小明完成证明；若不成立，请说明理由。
(3)、拓展应用如图(3)，在△ABC中，∠BAC= 90°，AB=AC=4，点D、E均在边BC上，且∠DAE=45°，若BD= ，请求出线段DE的长。
22. 如图
(1)、证明推断：如图(1)，在正方形ABCD中，点E、Q分别在边BC、AB上，DQ⊥AE于点O，点G、F分别在边CD、AB上，GF⊥AE。①填空：DQAE(填“>”“<”或“=”) ；
②推断： 的值为；
(2)、类比探究：如图(2)，在矩形ABCD中， =k(k为常数)。将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O。试探究GF与AE之间的数量关系，并说明理由；(3)、拓展应用：在(2)的条件下，连接CP，当k= 时，若 = ，GF= ，求CP的长。