广东省深圳市龙岗区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-02-02 类型:期末考试
一、选择题(本部分共10小题,每小题3分,共30分)
-
1. 方程x2=2x的解是( )A、x=2 B、x1=0 C、x1=0,x2=-2 D、x1=0,x2=22. 下面四个几何体中,主视图为三角形的是( )A、
 B、
B、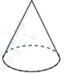 C、
C、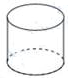 D、
D、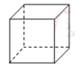 3. 如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )
3. 如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )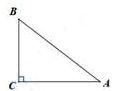 A、sinA= B、cosB= C、tanA= D、sinB=4. 将抛物线y=2x2先向左平移3个单位,再向上平移2个单位,得到的新抛物线对应的函数表达式是( )A、y=2(x+3)2+2 B、y=2(x-3)2+2 C、y=2(x+3)2-2 D、y=2(x-3)2-25. 函数y= 和y=kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )A、
A、sinA= B、cosB= C、tanA= D、sinB=4. 将抛物线y=2x2先向左平移3个单位,再向上平移2个单位,得到的新抛物线对应的函数表达式是( )A、y=2(x+3)2+2 B、y=2(x-3)2+2 C、y=2(x+3)2-2 D、y=2(x-3)2-25. 函数y= 和y=kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )A、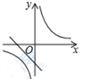 B、
B、 C、
C、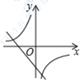 D、
D、 6. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在0.3左右,则袋子中红球的个数最有可能是( )A、14 B、12 C、6 D、47. 疫情促进了快递行业高速发展,某家快递公司2020年5月份与7月份完成投递的快递总件数分别为100万件和144万件,设该快递公司5月到7月投递总件数的月平均增长率为x,则下列方程正确的是( )A、100(1+2x)=144 B、100(1+x)2=144 C、100(1-2x)=144 D、100(1-x)2=1448. 下列命题中,错误的是( )A、顺次连接矩形四边的中点所得到的四边形是菱形 B、反比例函数的图象是轴对称图形 C、线段AB的长度是2,点C是线段AB的黄金分割点且AC<BC,则AC= -1 D、对于任意的实数b,方程x2-bx-3= 0有两个不相等的实数根9. 如图,在正方形ABCD中,E、F分别在CD、AD边上,且CE=DF,连接BE、CF相交于G点。则下列结论:①BE=CF;②S△BCG= S四边形DFGE;③CG2= BG·GE;④当E为CD中点时,连接DG,则∠FGD=45°。正确结论的个数是( )
6. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在0.3左右,则袋子中红球的个数最有可能是( )A、14 B、12 C、6 D、47. 疫情促进了快递行业高速发展,某家快递公司2020年5月份与7月份完成投递的快递总件数分别为100万件和144万件,设该快递公司5月到7月投递总件数的月平均增长率为x,则下列方程正确的是( )A、100(1+2x)=144 B、100(1+x)2=144 C、100(1-2x)=144 D、100(1-x)2=1448. 下列命题中,错误的是( )A、顺次连接矩形四边的中点所得到的四边形是菱形 B、反比例函数的图象是轴对称图形 C、线段AB的长度是2,点C是线段AB的黄金分割点且AC<BC,则AC= -1 D、对于任意的实数b,方程x2-bx-3= 0有两个不相等的实数根9. 如图,在正方形ABCD中,E、F分别在CD、AD边上,且CE=DF,连接BE、CF相交于G点。则下列结论:①BE=CF;②S△BCG= S四边形DFGE;③CG2= BG·GE;④当E为CD中点时,连接DG,则∠FGD=45°。正确结论的个数是( )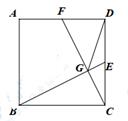 A、1 B、2 C、3 D、410. 如图,抛物线y=ax2+bx+c(a< 0)的图象经过点(1, 2),与x轴交点的横坐标分别为x1 , x2 , 其中-1<x1<0,1<x2<2, 则下列结论中正确的是( )
A、1 B、2 C、3 D、410. 如图,抛物线y=ax2+bx+c(a< 0)的图象经过点(1, 2),与x轴交点的横坐标分别为x1 , x2 , 其中-1<x1<0,1<x2<2, 则下列结论中正确的是( )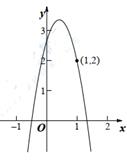 A、a<-1 B、b>2 C、2a+b> 0 D、k为任意实数,关于x的方程ax2 +bx+c+k2 = 0没有实数根
A、a<-1 B、b>2 C、2a+b> 0 D、k为任意实数,关于x的方程ax2 +bx+c+k2 = 0没有实数根二、填空题(本部分共5小题,每小题3分,共15分)
-
11. 已知 ,则 =。12. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且OE=EA,则 =。
 13. 对于实数a、b,定义新运算“ ”: a b=a2-ab,如4 2=42-4×2=8。若x 4=-4,则实数x的值是。14. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A (-5, 0),且tanA= ,反比例函数y= (k≠0)经过点C,则k的值是。
13. 对于实数a、b,定义新运算“ ”: a b=a2-ab,如4 2=42-4×2=8。若x 4=-4,则实数x的值是。14. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A (-5, 0),且tanA= ,反比例函数y= (k≠0)经过点C,则k的值是。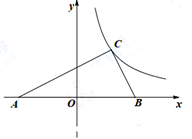 15. 已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是。
15. 已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是。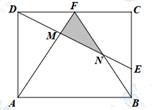
三、解答题(本大题共7题。其中16题5分,17题6分,18题6分,19题9分,20题9分,21题10分,22 题10分,共55分)
-
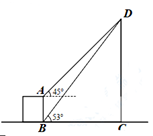
16. 计算:(-1)2021 + ·cos30°-( )-117. 在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字“-3, -2,1, 6”。(1)、随机抽出一张卡片是负数的概率是;(2)、第一次从袋中随机地抽出一张卡片,把所抽到的数字记为横坐标m,不放回袋中,再随机地从中抽出一张,把所抽到的数字记为纵坐标n。请用数状图或列表法求所得的点(m, n)在反比例函.数y= 上的概率。18. 如图,从楼层底部B处测得旗杆CD的顶端D处的仰角是53°,从楼层顶部A处测得旗杆CD的顶端D处的仰角是45°,已知楼层AB的楼高为3米。求旗杆CD的高度约为多少米?(参考数据: sin53°≈ ,cos53°≈ ,tan53°≈ )
 19. 如图,直线AD:y=3x+3与坐标轴交于A、D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点过点C的反比例函数y= (k≠0)与直线AD交于E、F两点。
19. 如图,直线AD:y=3x+3与坐标轴交于A、D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点过点C的反比例函数y= (k≠0)与直线AD交于E、F两点。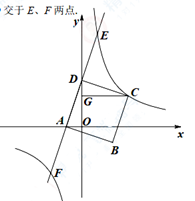 (1)、求证:△AOD≌ODGC;(2)、求E、F两点坐标;(3)、填空:不等式3x+3> 的取值范围是。20. 在新冠肺炎抗疫期间,某药店决定销售一批口罩,经市场调研:某类型口罩进价每包为20元,当售价为每包24元时,周销售量为160包,若售价每提高1元,周销售量就会减少10包。设该类型售价为x元(不低于进价),周利润为y元.请解答以下问题:(1)、求y与x的函数关系式?(要求关系式化为一般式)(2)、该药店为了获得周利润750元,且让利给顾客,售价应为多少元?(3)、物价局要求利润不得高于45%,当售价定为多少时,该药店获得利润最大,最大利润是多少元?21. 如图1, ABCD的对角线AC平分∠BAD,AB=6。点E从A点出发沿AB方向以1个单位/秒的速度运动,点F从C点出发沿CA方向以 个单位/秒的速度运动,其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒。
(1)、求证:△AOD≌ODGC;(2)、求E、F两点坐标;(3)、填空:不等式3x+3> 的取值范围是。20. 在新冠肺炎抗疫期间,某药店决定销售一批口罩,经市场调研:某类型口罩进价每包为20元,当售价为每包24元时,周销售量为160包,若售价每提高1元,周销售量就会减少10包。设该类型售价为x元(不低于进价),周利润为y元.请解答以下问题:(1)、求y与x的函数关系式?(要求关系式化为一般式)(2)、该药店为了获得周利润750元,且让利给顾客,售价应为多少元?(3)、物价局要求利润不得高于45%,当售价定为多少时,该药店获得利润最大,最大利润是多少元?21. 如图1, ABCD的对角线AC平分∠BAD,AB=6。点E从A点出发沿AB方向以1个单位/秒的速度运动,点F从C点出发沿CA方向以 个单位/秒的速度运动,其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒。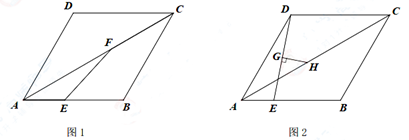 (1)、求证:四边形ABCD是菱形:(2)、若∠ABC=120°,试求t的值为多少时,△AEF为直角三角形;(3)、如图2,若∠ABC=120°,点G是DE是中点,作GH⊥DE交AC于H。当点E在AB边运动的过程中(不与点B重合),则线段GH的最大值是 , GH的最小值是。22. 已知抛物线y=ax2-3ax-4a(a<0)与x轴交于A B两点,与y轴交于C点。
(1)、求证:四边形ABCD是菱形:(2)、若∠ABC=120°,试求t的值为多少时,△AEF为直角三角形;(3)、如图2,若∠ABC=120°,点G是DE是中点,作GH⊥DE交AC于H。当点E在AB边运动的过程中(不与点B重合),则线段GH的最大值是 , GH的最小值是。22. 已知抛物线y=ax2-3ax-4a(a<0)与x轴交于A B两点,与y轴交于C点。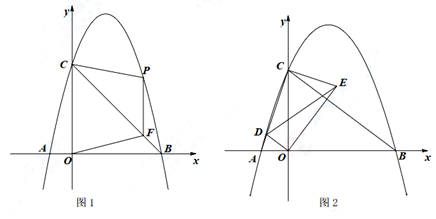 (1)、若a=-1时
(1)、若a=-1时①求A、B、C三点的坐标;
②如图1,点P是直线BC上方抛物线上一点,过P点作PF∥y轴交BC于F点,若 ,请求出P点坐标;
(2)、如图2,将△AOC绕原点0顺时针旋转得△DOE,且使得点D落在线段AC上。当OE⊥BC时,请求出a的值和CE的长。