广东省深圳市罗湖区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-02-02 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 化简 的结果是( )A、3 B、-3 C、±3 D、±92. 下列计算结果,正确的是( )A、 =-3 B、 + = C、 - =1 D、 =53. 下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )A、
 B、
B、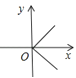 C、
C、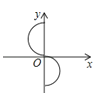 D、
D、 4. 点P(3,-5)关于y轴对称的点的坐标为( )A、(3,5) B、(-3,5) C、(-3,-5) D、(-5,3)5. 下列四组数据中,不能作为直角三角形的三边长的是( )A、6,8,10 B、10,15,20 C、5,12,13 D、7,24,256. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
4. 点P(3,-5)关于y轴对称的点的坐标为( )A、(3,5) B、(-3,5) C、(-3,-5) D、(-5,3)5. 下列四组数据中,不能作为直角三角形的三边长的是( )A、6,8,10 B、10,15,20 C、5,12,13 D、7,24,256. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )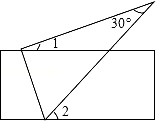 A、30° B、40° C、50° D、60°7. 下列说法正确的是( )A、一个游戏中奖的概率是 ,则玩100次这样的游戏一定会中奖 B、为了解全国中学生的心理健康状况,应采用普查的方式 C、一组数据0,1,2,1,1的众数和中位数都是1 D、若甲组数据的方差 =0.2,乙组数据的方差 =0.5,则乙组数据比甲组数据稳定8. 一次函数y=kx+b , 经过(1,1),(2,4),则k与b的值为( )A、 B、 C、 D、9. 直角三角形的两条直角边长为a , b , 斜边上的高为h , 则下列各式中总能成立的是( )A、ab=h2 B、a2+b2=2h2 C、 + = D、 + =10. 如图,已知△ABC中,AB=AC , AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G . 下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2 . 其中正确结论的个数是( )
A、30° B、40° C、50° D、60°7. 下列说法正确的是( )A、一个游戏中奖的概率是 ,则玩100次这样的游戏一定会中奖 B、为了解全国中学生的心理健康状况,应采用普查的方式 C、一组数据0,1,2,1,1的众数和中位数都是1 D、若甲组数据的方差 =0.2,乙组数据的方差 =0.5,则乙组数据比甲组数据稳定8. 一次函数y=kx+b , 经过(1,1),(2,4),则k与b的值为( )A、 B、 C、 D、9. 直角三角形的两条直角边长为a , b , 斜边上的高为h , 则下列各式中总能成立的是( )A、ab=h2 B、a2+b2=2h2 C、 + = D、 + =10. 如图,已知△ABC中,AB=AC , AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G . 下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2 . 其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题3分,共15分)
-
11. = .12. 已知点A(m , -2),B(3,m-1),且直线AB∥x轴,则m的值是 .13. 如图,在△ABC中,∠A=50°,BE平分∠ABC , CE平分外角∠ACD , 则∠E的度数为 .
 14. 若一个正数m的两个平方根分别是a-1和4-2a , 则m的值为 .15. 如图,正方形ABCD的边长为4,点E为CD中点,点F为BC边上一点,且CF=1,连接AF , EG⊥AF交BC于点G , 则BG= .
14. 若一个正数m的两个平方根分别是a-1和4-2a , 则m的值为 .15. 如图,正方形ABCD的边长为4,点E为CD中点,点F为BC边上一点,且CF=1,连接AF , EG⊥AF交BC于点G , 则BG= .
三、解答题(共55分)
-
16. 计算:(1)、( + )( - )+(2)、 -3× + -(π+1)0×17. 解方程组: .18. 某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).

回答下列问题:
(1)、这次调查一共抽查了名学生的植树量;请将条形图补充完整;(2)、被调查学生每人植树量的众数是棵、中位数是棵;(3)、求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?19. 如图,点C , B , E在同一条直线上,AC⊥BC , BD⊥DE , BC=ED=6,BE=10,∠BAC=∠DBE . (1)、求证:△ABC≌△BED;(2)、求△ABD的面积.20. 某景点的门票价格如下表:
(1)、求证:△ABC≌△BED;(2)、求△ABD的面积.20. 某景点的门票价格如下表:购票人数
1~50
51~100
100以上
每人门票价
20
16
10
某校八年级(一)、(二)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1828元,如果两班联合起来作为一个团体购票,则只需花费1020元.
(1)、两个班各有多少名学生?(2)、团体购票与单独购票相比较,两个班各节约了多少元?21. 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0),B点坐标是(-3,1),C点坐标是(-2,3). (1)、作△ABC关于y轴对称的图形△DEF , 其中A、B、C的对应点分别为D、E、F;(2)、动点P的坐标为(0,t),当t为何值时,PA+PC的值最小,并写出PA+PC的最小值;(3)、在(1)的条件下,点Q为x轴上的动点,当△QDE为等腰三角形,请直接写出Q点的坐标.22. 如图1,直线AB:y= x+4分别与x轴、y轴交于A、B两点,过点B的直线交x轴负半轴于点C , 将△BOC沿BC折叠,使点O落在BA上的点M处.
(1)、作△ABC关于y轴对称的图形△DEF , 其中A、B、C的对应点分别为D、E、F;(2)、动点P的坐标为(0,t),当t为何值时,PA+PC的值最小,并写出PA+PC的最小值;(3)、在(1)的条件下,点Q为x轴上的动点,当△QDE为等腰三角形,请直接写出Q点的坐标.22. 如图1,直线AB:y= x+4分别与x轴、y轴交于A、B两点,过点B的直线交x轴负半轴于点C , 将△BOC沿BC折叠,使点O落在BA上的点M处. (1)、求A、B两点的坐标;(2)、求线段BC的长;(3)、点P为x轴上的动点,当∠PBA=45°时,求点P的坐标.
(1)、求A、B两点的坐标;(2)、求线段BC的长;(3)、点P为x轴上的动点,当∠PBA=45°时,求点P的坐标.