广东省深圳市龙岗区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-02-02 类型：期末考试

进入出卷网下载

一、选择题（本部分共10小题，每小题3分，共30分。）

1. 以下列各组数据为三角形三边，能构成直角三角形的是（）

A、4cm，8cm，7cm B、3cm，5cm，2cm C、2cm，2cm，4cm D、13cm，12cm，5cm

查看试题解析
2. 在实数 $\sqrt{5}$ 、3.1415、π、 $\sqrt{144}$ 、 $\sqrt[3]{6}$ 、2.123122312223……（1和3之间的2逐次加1个）中，无理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列叙述正确的是（）

A、 $\sqrt{{(- 2)}^{2}}$ ＝﹣2 B、12 $\frac{1}{4}$ 的算术平方根是 $\frac{7}{2}$ C、 $\sqrt{16}$ ＝±4 D、（﹣π）²的平方根是π

查看试题解析
4. 平面直角坐标系中，点A（﹣2，1）到x轴的距离为（）

A、﹣2 B、1 C、2 D、 $\sqrt{5}$

查看试题解析
5. 下列方程组中不是二元一次方程组的是（）

A、 ${\begin{cases} s + 1 = 3 \\ 2 s - t = 4 \end{cases}$ B、 ${\begin{cases} m + n = 3 \\ 2 m - n = 4 \end{cases}$ C、 ${\begin{cases} x = 3 \\ y = 4 \end{cases}$ D、 ${\begin{cases} x + y = 3 \\ 2 x y - y = 4 \end{cases}$

查看试题解析
6. 如图是甲、乙两名射击运动员10次射击成绩的折线统计图，根据折线图判断下列说法正确的是（）

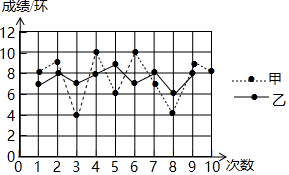A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、无法判断谁的成绩更稳定

查看试题解析
7. 下列命题中，是假命题的是（）

A、对顶角相等 B、两点之间，线段最短 C、互补的两个角不一定相等 D、同位角相等

查看试题解析
8. 在同一直角坐标系中，一次函数y＝kx+b和y＝bx+k的图象可能正确的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，AB∥CD，∠BAE＝120°，∠DCE＝30°，则∠AEC＝（）度．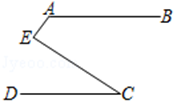

A、70 B、150 C、90 D、100

查看试题解析
10. 如图，已知直线AB：y＝ $\frac{\sqrt{55}}{3} x + \sqrt{55}$ 分别交x轴、y轴于点B、A两点，C（3，0），D、E分别为线段AO和线段AC上一动点，BE交y轴于点H，且AD＝CE．当BD+BE的值最小时，则H点的坐标为（）

A、 $(0 ， \frac{\sqrt{55}}{2})$ B、（0，5） C、（0，4） D、 $(0 ， \sqrt{55})$

查看试题解析

二、填空题（本部分共5小题，每小题3分，共15分，请将正确的答案填在答题卡上）

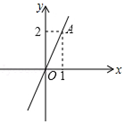
11. ﹣ $\sqrt{2}$ 的相反数是， $\sqrt{2}$ 的倒数是， $- \frac{1}{8}$ 的立方根是。

查看试题解析
12. 如图，将直线OA向上平移2个单位长度，则平移后的直线的表达式为。

查看试题解析
13. 已知方程组 ${\begin{cases} 3 a + b = 4 \\ a - 2 b = 1 \end{cases}$ ，则2a+3b的值是。

查看试题解析
14. 如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是cm．

查看试题解析
15. 如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：
第一次操作，分别作∠ABE和∠DCE的平分线，交点为E₁ ，

第二次操作，分别作∠ABE₁和∠DCE₁的平分线，交点为E₂ ，

第三次操作，分别作∠ABE₂和∠DCE₂的平分线，交点为E₃ ， …，

第n次操作，分别作∠ABE_n_﹣1和∠DCE_n_﹣1的平分线，交点为E_n ．

若∠E_n＝1度，那∠BEC等于度。

查看试题解析

三、解答题（本大题共7题。其中16题5分，17题10分，18题7分，19题7分，20题9分，21题8分，22题9分，共55分）

16. 计算： ${(- 2)}^{2} - {(π - 1)}^{0} - \sqrt{9} + | \sqrt{2} - 3 |$ ．

查看试题解析
17. 解方程（组）：

(1)、 ${\begin{cases} x - y = 3 \\ 4 x + 3 y = 5 \end{cases}$ ；

(2)、 ${\begin{cases} \frac{x + 2}{2} + \frac{2 y + 5}{3} = 5 \\ 3 x - 4 y = - 2 \end{cases}$ ．

查看试题解析

18. 某校为了解八年级学生课外阅读情况，随机抽取20名学生平均每周用于课外阅读的时间（单位：min），过程如表；

【收集数据】

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

【整理数据】

课外阅读时间x（min）	0≤x＜40	40≤x＜80	80≤x＜120	120≤x＜160
等级	D	C	B	A
人数	3	a	8	b

【分析数据】

平均数	中位数	众数
80	m	n

请根据以上提供的信息，解答下列问题：

(1)、填空：a＝， b＝， m＝， n＝；

(2)、如果每周用于课外阅读的时间不少于80min为达标，该校八年级现有学生800人，估计八年级达标的学生有多少人？

查看试题解析

19. 某工厂用如图①所示的长方形和正方形纸板，做成如图②所示的竖式与横式两种长方体的无盖纸盒．现有正方形纸板150张，长方形纸板300张，若这些纸板恰好用完，则可制作横式、竖式两种纸盒各多少个？

查看试题解析
20. 如图，在平面直角坐标系中，过点C（0，6）的直线AC与直线OA相交于点A（4，2）．

(1)、求直线AC的表达式；

(2)、求△OAC的面积；

(3)、动点M在线段OA和射线AC上运动，是否存在点M，使△OMC的面积是△OAC的面积的 $\frac{1}{2}$ ？若存在，求出此时点M的坐标；若不存在，请说明理由。

查看试题解析
21. 如图，已知AM∥BN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

(1)、∠ABN的度数是， ∠CBD的度数是；

(2)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；

(3)、当点P运动到使∠ACB＝∠ABD时，∠ABC的度数是多少？

查看试题解析
22. 点P是平面直角坐标系中的一点且不在坐标轴上，过点P向x轴，y轴作垂线段，若垂线段的长度的和为4，则点P叫做“垂距点”，例如：如图中的P（1，3）是“垂距点”。
（备用图）

(1)、在点A（2，2），B（ $\frac{3}{2}$ ，﹣ $\frac{5}{2}$ ），C（﹣1，5），是“垂距点”的为；

(2)、若D（ $\frac{3}{2}$ m， $\frac{1}{2}$ m）为“垂距点”，求m的值；

(3)、若过点（2，3）的一次函数y＝kx+b（k≠0）的图象上存在“垂距点”，则k的取值范围是．

查看试题解析