广东省深圳市福田区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-02-02 类型:期末考试
一、选择题。(本大题共12小题,每小题3分,共36分)
-
1. 下列各式中,正确的是( )A、 B、 C、 D、2. 设 为正整数,且 ,则 的值为( )A、7 B、8 C、9 D、103. 如图 ,阴影部分是一个长方形,则长方形的面积是( )
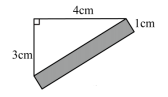 A、 B、 C、 D、4. 在广东省某公路上,一辆小轿车和一辆货车沿相同的路线从 地到 地,所经过的路程 (千米)与时间 (小时)的函数关系如图所示,小轿车比货车早到( )
A、 B、 C、 D、4. 在广东省某公路上,一辆小轿车和一辆货车沿相同的路线从 地到 地,所经过的路程 (千米)与时间 (小时)的函数关系如图所示,小轿车比货车早到( ) A、1 小时 B、2 小时 C、3 小时 D、4 小时5. 下列四个命题中,真命题有( )
A、1 小时 B、2 小时 C、3 小时 D、4 小时5. 下列四个命题中,真命题有( )①两条直线被第三条直线所截,内错角相等;②如果 和 是对顶角,那么 ;③三角形的一个外角大于任何一个内角;④如果 ,那么 .
A、1 个 B、2 个 C、3 个 D、4 个6. 已知平面直角坐标系有一点 ,无论 取何值,点 不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图 , , 交 于点 , , ,则 的度数为( ) A、 B、 C、 D、8. 如图 ,若弹簧的总长度 是关于所挂重物 的一次函数 ,则不挂重物时, 弹簧的长度是( )
A、 B、 C、 D、8. 如图 ,若弹簧的总长度 是关于所挂重物 的一次函数 ,则不挂重物时, 弹簧的长度是( ) A、5cm B、8cm C、9cm D、10cm9. 中国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之。余绳四尺五,屈绳 量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余 4.5 尺,将绳 子对折再量木条,木条剩余 1 尺,问木条多少尺?”设绳子长 尺,木条 尺,根据题意所列方程 正确的是( )A、 B、 C、 D、10. 如图,长方形ABCD是由6个正方形组成,其中有两个一样大的正方形,且最小正方形边长为1,则长方形ABCD的边长DC为( )
A、5cm B、8cm C、9cm D、10cm9. 中国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之。余绳四尺五,屈绳 量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余 4.5 尺,将绳 子对折再量木条,木条剩余 1 尺,问木条多少尺?”设绳子长 尺,木条 尺,根据题意所列方程 正确的是( )A、 B、 C、 D、10. 如图,长方形ABCD是由6个正方形组成,其中有两个一样大的正方形,且最小正方形边长为1,则长方形ABCD的边长DC为( )
 A、10 B、13 C、16 D、1911. 如图 ,长方形 中,点 是 中点, 是 边上的点,把 沿 折叠后,点 恰 好与点 重合,则图中全等的三角形有( )对。
A、10 B、13 C、16 D、1911. 如图 ,长方形 中,点 是 中点, 是 边上的点,把 沿 折叠后,点 恰 好与点 重合,则图中全等的三角形有( )对。 A、1 B、2 C、3 D、412. 已知,如图 , 为线段 上一动点(不与点 , 重合),在 同侧分别作等边三角形 和等边三角形 , 与 交于点 , 与 交于点 , 与 交于点 ,连结 , , ,以下四个结论:① ;②三角形 是等边三角形;③ ;④ 平分 ,其中正确的结论是( )
A、1 B、2 C、3 D、412. 已知,如图 , 为线段 上一动点(不与点 , 重合),在 同侧分别作等边三角形 和等边三角形 , 与 交于点 , 与 交于点 , 与 交于点 ,连结 , , ,以下四个结论:① ;②三角形 是等边三角形;③ ;④ 平分 ,其中正确的结论是( ) A、①② B、③④ C、①②③ D、①②④
A、①② B、③④ C、①②③ D、①②④二、填空题(本大题共4小题,每小题3分,共12分)
-
13. 小明某学期的数学平时成绩90分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时成绩:期中成绩:期末成绩3:3:4,则小明总评成绩是分.14. 如图,长方体的长为15,宽为10,高为20,点 离点 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是 .
 15. 如图是“赵爽弦图”, , , 和 是四个全等的直角三角形,四边形 和 都是正方形,如果 ,且 ,那么 等于 .
15. 如图是“赵爽弦图”, , , 和 是四个全等的直角三角形,四边形 和 都是正方形,如果 ,且 ,那么 等于 . 16. 如图,在平面直角坐标系中,点 ,点 ,点 在直线 上,且 ,则点 坐标为( , ).
16. 如图,在平面直角坐标系中,点 ,点 ,点 在直线 上,且 ,则点 坐标为( , ).
三、解答题(本大题共7小题,其中,17题7分,18题8分,19题7分,20题6分,21题7分,22题7分,23题10分,共52分)
-
17. 计算:(1)、(2)、18. 解下列方程组:(1)、(2)、19. 福田区某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:
 (1)、九(1)班复赛成绩的中位数是分,九(2)班复赛成绩的众数是分;(2)、小明同学已经算出了九(1)班复赛的平均成绩 ,方差 ,请你求出九(2)班复赛的平均成绩 和方差 ;(3)、根据(2)中计算结果,分析哪个班级的复赛成绩较好?20. 作图题, 为格点三角形,即 三个顶点落在格点上.(不要求写作法)
(1)、九(1)班复赛成绩的中位数是分,九(2)班复赛成绩的众数是分;(2)、小明同学已经算出了九(1)班复赛的平均成绩 ,方差 ,请你求出九(2)班复赛的平均成绩 和方差 ;(3)、根据(2)中计算结果,分析哪个班级的复赛成绩较好?20. 作图题, 为格点三角形,即 三个顶点落在格点上.(不要求写作法)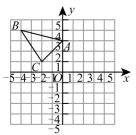
⑴请在坐标系内用直尺画出 ,使 与 关于 轴对称;
⑵请在坐标系内用直尺画出 ,使 与 关于 轴对称。
21. 如图,在 中, ,平分 ,交 于点 ,过点 作 于点 .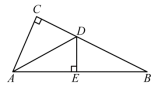 (1)、求证: ;(2)、若 ,且 ,求 的长.
(1)、求证: ;(2)、若 ,且 ,求 的长.
