河北省唐山市路南区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 如果2是一元二次方程 的一个根,那么常数c是( )A、2 B、-2 C、4 D、-42. 如图,两个同心圆中有两条互相垂直的直径,其中大圆的半径是2,则图中阴影部分的面积是( )
 A、 B、 C、 D、3. 用配方法解方程x2﹣6x﹣3=0,此方程可变形为( )A、(x﹣3)2=3 B、(x﹣3)2=6 C、(x+3)2=12 D、(x﹣3)2=124. 在图形的旋转中,下列说法错误的是( )A、旋转前和旋转后的图形全等 B、图形上的每一个点到旋转中心的距离都相等 C、图形上的每一个点旋转的角度都相同 D、图形上可能存在不动的点5. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )A、6 B、8 C、12 D、106. 点 关于原点对称点的坐标是( )A、 B、 C、 D、7. 如图;四边形 的四个顶点均在半圆O上,若 ,则 ( )
A、 B、 C、 D、3. 用配方法解方程x2﹣6x﹣3=0,此方程可变形为( )A、(x﹣3)2=3 B、(x﹣3)2=6 C、(x+3)2=12 D、(x﹣3)2=124. 在图形的旋转中,下列说法错误的是( )A、旋转前和旋转后的图形全等 B、图形上的每一个点到旋转中心的距离都相等 C、图形上的每一个点旋转的角度都相同 D、图形上可能存在不动的点5. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )A、6 B、8 C、12 D、106. 点 关于原点对称点的坐标是( )A、 B、 C、 D、7. 如图;四边形 的四个顶点均在半圆O上,若 ,则 ( )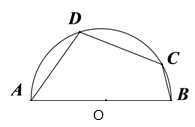 A、130° B、120° C、125° D、110°8. 已知 是关于x的一元二次方程,则实数m的取值范围是( )A、 B、 C、 D、9. 将 绕点O旋转 得到 ,则下列作图正确的是( )A、
A、130° B、120° C、125° D、110°8. 已知 是关于x的一元二次方程,则实数m的取值范围是( )A、 B、 C、 D、9. 将 绕点O旋转 得到 ,则下列作图正确的是( )A、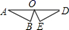 B、
B、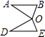 C、
C、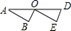 D、
D、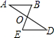 10. 下列各图象中有可能是函数 的图象( )A、
10. 下列各图象中有可能是函数 的图象( )A、 B、
B、 C、
C、 D、
D、 11. 某中学准备建一个面积为5000平方米的矩形操场,操场的长比宽长50米,设操场的长为x米,根据题意,下面所列方程正确的是( )A、 B、 C、 D、12. 当一个三角形的内心与外心重合时,这个三角形一定是( )A、直角三角形 B、等腰直角三角形 C、钝角三角形 D、等边三角形13. 对于二次函数 的图象,下列说法中错误的是( )A、顶点是 B、开口向上 C、与x轴有两个交点 D、对称轴是14. 在 中, , , ,将 绕边 所在直线旋转一周得到一个圆锥,该圆锥的侧面积( )A、 B、 C、 D、15. 如图,将函数 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
11. 某中学准备建一个面积为5000平方米的矩形操场,操场的长比宽长50米,设操场的长为x米,根据题意,下面所列方程正确的是( )A、 B、 C、 D、12. 当一个三角形的内心与外心重合时,这个三角形一定是( )A、直角三角形 B、等腰直角三角形 C、钝角三角形 D、等边三角形13. 对于二次函数 的图象,下列说法中错误的是( )A、顶点是 B、开口向上 C、与x轴有两个交点 D、对称轴是14. 在 中, , , ,将 绕边 所在直线旋转一周得到一个圆锥,该圆锥的侧面积( )A、 B、 C、 D、15. 如图,将函数 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 在 中,弧 的度数为60°,则弧 所对的圆心角的度数为 .17. 关于x的一元二次方程有两个根0和3,写出这个一元二次方程的一个一般式为 .18. 如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,则bc的值为(填正或负).
 19. 如图,已知⊙O是以数轴上原点O为圆心,半径为2的圆,∠AOB=45°,点P在x正半轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P点对应的数为x,则x的取值范围是 .
19. 如图,已知⊙O是以数轴上原点O为圆心,半径为2的圆,∠AOB=45°,点P在x正半轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P点对应的数为x,则x的取值范围是 .
三、解答题
-
20. 解方程:(1)、 ;(2)、 .21. 如图,长梯AB斜靠在墙壁上,梯脚B距墙80 cm,梯上点D距墙70 cm,量得BD长55 cm,求梯子的长.
 22. 已知二次函数y=ax2与y=﹣2x2+c.(1)、随着系数a和c的变化,分别说出这两个二次函数图象的变与不变;(2)、若这两个函数图象的形状相同,则a=;若抛物线y=ax2沿y轴向下平移2个单位就能与y=﹣2x2+c的图象完全重合,则c=;(3)、二次函数y=﹣2x2+c中x、y的几组对应值如表:
22. 已知二次函数y=ax2与y=﹣2x2+c.(1)、随着系数a和c的变化,分别说出这两个二次函数图象的变与不变;(2)、若这两个函数图象的形状相同,则a=;若抛物线y=ax2沿y轴向下平移2个单位就能与y=﹣2x2+c的图象完全重合,则c=;(3)、二次函数y=﹣2x2+c中x、y的几组对应值如表:x
﹣2
1
5
y
m
n
p
表中m、n、p的大小关系为(用“<”连接).
23. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在⊙O上,若∠AOD=50°. (1)、求∠DEB的度数;(2)、若OC=3,OA=5,
(1)、求∠DEB的度数;(2)、若OC=3,OA=5,①求弦AB的长;
②求劣弧AB的长.
24. 某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.(1)、当某天客房全部住满时,这天客房收入为元;(2)、设每间客房每天的定价增加m元,则宾馆出租的客房为间;(3)、如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?25. 已知 是边长为4的等边三角形,边 在射线 上,且 ,点D是射线 上的动点,当点D不与点A重合时,将 绕点C逆时针方向旋转60°得到 ,连接 . (1)、如图1,求证: 是等边三角形.(2)、设 ,
(1)、如图1,求证: 是等边三角形.(2)、设 ,①如图2,当 时, 的周长存在最小值,请求出此最小值;
②如图1,若 ,直接写出以D、E、B为顶点的三角形是直角三角形时t的值.
26. 在平面直角坐标系 中,抛物线 与x轴交于点A、B.(1)、①求m的取值范围;②当抛物线经过原点时,求抛物线的解析式;
③求抛物线的顶点坐标;
(2)、若线段 上有且只有5个点的横坐标为整数,求m的取值范围;(3)、若抛物线在 这一段位于x轴下方,在 这一段位于x轴上方,求m的值.