河北省石家庄市新乐市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-02-02 类型:期中考试
一、单选题
-
1. 下列各组中的四条线段是成比例线段的是( )A、4cm,4cm,5cm,6cm B、1cm,2cm,3cm,5cm C、3cm,4cm,5cm,6cm D、1cm,2cm,2cm,4cm2. 把一元二次方程 化为一般形式正确的是( )A、 B、 C、 D、3. 小明拿 米的竹竿立于地面,测其影长为 米,同一时刻测得一棵树在太阳光下的影长为 米,则这棵树的高为( )A、7.2米 B、8.64米 C、6米 D、6.48米4. 图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到( )
 A、轴对称 B、平移 C、旋转 D、相似5. 公式法解方程x2﹣3x﹣4=0,对应a,b,c的值分别是( )A、1,3,4 B、0、﹣3、﹣4 C、1、3、﹣4 D、1、﹣3、﹣46. 若m , n是方程x2+2019x﹣2020=0的两个实数根,则m+n﹣mn的值为( )A、﹣4039 B、﹣1 C、1 D、40397. 用配方法解方程x2+4x=6,下列配方正确的是( )A、 B、 C、 D、8. 某校在计算学生的数学期评成绩时,规定期中考试成绩占40%,期末考试成绩占60%.王林同学的期中数学考试成绩为80分,期末数学考试成绩为90分,那么他的数学期评成绩是( )A、80分 B、82分 C、84分 D、86分9. 两个相似三角形的面积之比为 ,则这两个三角形的周长比为( )A、 B、 C、 D、10. 若关于 的一元二次方程 的一个根为 ,则 的值为( )A、 B、 或 C、 D、11. 如图所示,点B是线段AC的黄金分割点 ,则下列结论中,正确的是( ).
A、轴对称 B、平移 C、旋转 D、相似5. 公式法解方程x2﹣3x﹣4=0,对应a,b,c的值分别是( )A、1,3,4 B、0、﹣3、﹣4 C、1、3、﹣4 D、1、﹣3、﹣46. 若m , n是方程x2+2019x﹣2020=0的两个实数根,则m+n﹣mn的值为( )A、﹣4039 B、﹣1 C、1 D、40397. 用配方法解方程x2+4x=6,下列配方正确的是( )A、 B、 C、 D、8. 某校在计算学生的数学期评成绩时,规定期中考试成绩占40%,期末考试成绩占60%.王林同学的期中数学考试成绩为80分,期末数学考试成绩为90分,那么他的数学期评成绩是( )A、80分 B、82分 C、84分 D、86分9. 两个相似三角形的面积之比为 ,则这两个三角形的周长比为( )A、 B、 C、 D、10. 若关于 的一元二次方程 的一个根为 ,则 的值为( )A、 B、 或 C、 D、11. 如图所示,点B是线段AC的黄金分割点 ,则下列结论中,正确的是( ).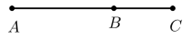 A、 B、 C、 D、12. 若 ,则 的值是( )A、0.5 B、 C、2 D、13. 如图, 中, ,则下列等式中不成立的是( )
A、 B、 C、 D、12. 若 ,则 的值是( )A、0.5 B、 C、2 D、13. 如图, 中, ,则下列等式中不成立的是( )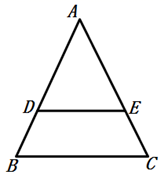 A、 B、 C、 D、14. 某班每位学生上、下学期各选择一个社团,下表分别为该班学生上、下学期各社团的人数比例.若该班上、下学期的学生人数不变,关于上学期,下学期各社团的学生人数变化,下列叙述正确的是( )
A、 B、 C、 D、14. 某班每位学生上、下学期各选择一个社团,下表分别为该班学生上、下学期各社团的人数比例.若该班上、下学期的学生人数不变,关于上学期,下学期各社团的学生人数变化,下列叙述正确的是( )文学社
篮球社
动漫社
上学期
3
4
5
下学期
4
3
2
A、文学社增加,篮球社不变 B、文学社不变,篮球社不变 C、文学社增加,篮球社减少 D、文学社不变,篮球社减少15. 已知5个数a1、a2、a3、a4、a5的平均数是a,则数据a1+1,a2+2,a3+3,a4+4,a5+5的平均数为( )A、a B、a+3 C、 a D、a+1516. 如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )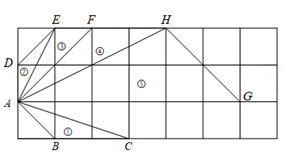 A、②④ B、②⑤ C、③④ D、④⑤
A、②④ B、②⑤ C、③④ D、④⑤二、填空题
-
17. 方程 的根是 .18. 如图,添加一个条件: , 使△ADE∽△ACB,(写出一个即可)
 19. 如图,在正方形 中,E是边 的中点,F是边 上异于B,C的一点.
19. 如图,在正方形 中,E是边 的中点,F是边 上异于B,C的一点.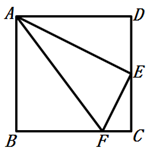
⑴若 ,则 ;
⑵若 ,则 ;
⑶当 与 满足数量关系时, .
三、解答题
-
20.(1)、解方程 (直接开平方法)(2)、若关于x的一元二次方程 的常数项为0,求m的值.21. 为响应我市创建“全国文明城市”的号召,我区某校举办了一次“秀美巴中,绿色家园”主题演讲比赛,满分 分,得分均为整数,成绩大于等于 分为合格,大于等于 分为优秀,这次演讲比赛中甲、乙两组学生(各 名学生)成绩分布的条形统计图如下图:
 (1)、补充完成下列的成绩统计分析表:
(1)、补充完成下列的成绩统计分析表:组别
平均分
中位数
众数
方差
合格率
优秀率
甲
乙
(2)、小王同学说:“这次演讲赛我得了 分,在我们小组中排名属中游略偏上!”观察上表可知,小王是组的学生;(填“甲”或“乙”)(3)、结合两个小组的成绩分析,你觉得哪个组的成绩更好一些?说说你的理由.22. 如图,在 中,点D在 边上, ,求证: . 23. 如图,在阳光下,旗杆 在地面上的影长 为 ,在建筑物墙面上的影长 为 ,同一时刻,测得直立于地面长 的木杆的影长为 ,求旗杆 的高度.
23. 如图,在阳光下,旗杆 在地面上的影长 为 ,在建筑物墙面上的影长 为 ,同一时刻,测得直立于地面长 的木杆的影长为 ,求旗杆 的高度.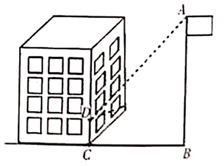 24. 卫生部疾病控制专家经过调研提出,如果1人传播10人以上而且被传染的人已经确定为非典型肺炎,那么这个传播者就可以称为“超级传播者”.如果某镇有1人不幸成为新冠肺炎病毒的携带者,假设每轮传染的人数相同,经过两轮传染后共有169成为新冠肺炎病毒的携带者.(1)、经过计算,判断最初的这名病毒的携带者是“超级传播者”吗?写出过程.(2)、若不加以控制传染渠道,经过3轮传染,共有多少人成为新冠肺炎病毒的携带者?25. 如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
24. 卫生部疾病控制专家经过调研提出,如果1人传播10人以上而且被传染的人已经确定为非典型肺炎,那么这个传播者就可以称为“超级传播者”.如果某镇有1人不幸成为新冠肺炎病毒的携带者,假设每轮传染的人数相同,经过两轮传染后共有169成为新冠肺炎病毒的携带者.(1)、经过计算,判断最初的这名病毒的携带者是“超级传播者”吗?写出过程.(2)、若不加以控制传染渠道,经过3轮传染,共有多少人成为新冠肺炎病毒的携带者?25. 如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.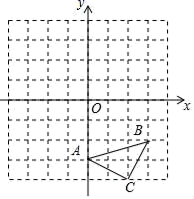
⑴画出△ABC向上平移4个单位得到的△A1B1C1;
⑵以点C为位似中心,在网格中画出△A2B2C , 使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
26. 如图,在△ABC中,∠B=90°,AB=6cm , BC=8cm . 点P从点A开始沿边AB向点B以每秒1cm的速度移动,点Q从点B开始沿边BC向点C以每秒2cm的速度移动,点P , Q分别从点A , B同时出发,且当一点到达终点时,另一点也停止运动.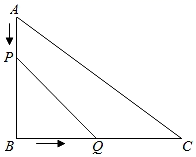 (1)、经过多少秒,可使PBQ的面积等于8cm2?(2)、经过多少秒,△ABC与△PBQ相似?(3)、线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(1)、经过多少秒,可使PBQ的面积等于8cm2?(2)、经过多少秒,△ABC与△PBQ相似?(3)、线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.