河北省邯郸市永年区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-02-02 类型：期中考试

进入出卷网下载

一、单选题

1. 方程x（x+5）＝0化成一般形式后，它的常数项是（）

A、﹣5 B、5 C、0 D、1

查看试题解析
2. 数轴上两点A、C表示的数分别为-2，6，以 $A C$ 为对角线做菱形 $A B C D$ ，连接 $B D$ 交 $A C$ 于O点，则O点所表示的数为（）

A、－1 B、1 C、2 D、3

查看试题解析
3. 将点 $A (3 ， 3)$ 向左平移4个单位长度得点 $A^{'}$ ，则点 $A^{'}$ 的坐标是（）

A、 $(- 1 ， - 1)$ B、 $(- 1 ， 3)$ C、 $(3 ， - 1)$ D、 $(7 ， 3)$

查看试题解析
4. 把△ABC三边的长度都扩大为原来的2倍，则锐角A的正切函数值（　　）

A、缩小为原来的 $\frac{1}{2}$ B、不变 C、扩大为原来的2倍 D、扩大为原来的4倍

查看试题解析
5. 如图：已知 $A D // B E // C F$ ，若 $A B = D E$ ，则（）

A、 $A B = B C$ B、 $B C = A D$ C、 $B C = E F$ D、 $A B = E F$

查看试题解析
6. 一元二次方程 $x^{2} - 4 x = 2$ 配方后化为 ${(x - 2)}^{2} = a$ ，则a的值为（）

A、18 B、10 C、6 D、4

查看试题解析
7. 如图所示，河堤横断面迎水坡 $A B$ 的坡度是1：2，点D是 $A C$ 的中点，则 $∠ B D C$ 的度数为（）

A、30° B、40° C、45° D、60°

查看试题解析
8. 在平面直角坐标系中，从原点O引一条射线，设这条射线与x轴的正半轴的夹角为 $α$ ，若 $\cos α$ = $\frac{3}{5}$ ，则这条射线是（）

A、OA B、OB C、OC D、OD

查看试题解析
9. 佳佳同学在解一元二次方程 $3 x^{2} - 8 x (x - 2) = 0$ 时，他是这样做的：
解： $3 x^{2} - 8 x (x - 2) = 0$

$3 x - 8 (x - 2) = 0$ ………………第一步

$- 5 x + 16 = 0$ ……………………第二步

$- 5 x = 16$ …………………………第三步

$x = - \frac{5}{16}$ …………………………第四步

小明的解法开始出现错误是从（）

A、第一步 B、第二步 C、第三步 D、第四步

查看试题解析
10. 在同一水平线上有两个观测点P、Q，从点P观测R点，俯角为30°，从点Q观测R点，俯角为45°，则符合条件的示意图是（）

A、 B、 C、 D、

查看试题解析
11. 下列调查中，最适合采用抽样调查的是（）

A、了解某批次灯泡的使用寿命情况 B、了解全班同学每周体育锻炼的时间 C、企业招聘，对应聘人员的面试 D、在“新冠状肺炎”疫情期间，对出入某小区的人员进行体温检测

查看试题解析
12. 某单位要招聘1名英语翻译，张明参加招聘考试的成绩如表所示：若把听、说、读、写的成绩按3：3：2：2计算平均成绩，则张明的平均成绩为（）

听

说

读

写

张明

90

80

83

82

A、82 B、83 C、84 D、85

查看试题解析
13. 某商场统计五个月来两种型号洗衣机的销售情况，制成了条形统计图，则在五个月中，下列说法正确的是（）

A、甲销售量比乙销售量稳定 B、乙销售量比甲销售量稳定 C、甲销售量与乙销售量一样稳定 D、无法比较两种洗衣机销售量稳定性

查看试题解析
14. 将矩形按照如图所示的方式向外扩张得到新矩形，每条对角线向其延长线两个方向各延伸 $a (a > 0)$ ，若所得新矩形与原矩形相似，则a的值的个数可以是（）

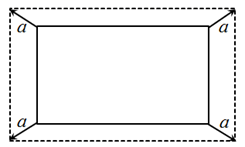A、1 B、2 C、3 D、无数个

查看试题解析

二、填空题

15. 关于x的一元二次方程 $a x^{2} + b x + 2 = 0 (a \neq 0)$ 的解是 $x = 1$ ，那么 $2 - a - b$ 的值是．

查看试题解析
16. 为了解居民用水情况，小明在某小区随机抽查了20户家庭的月用水量，结果如下表:

月用水量 $(m^{3})$

$4$

$5$

$6$

$8$

$9$

户数

$4$

$6$

$5$

$4$

$1$

则这20户家庭的月用水量的众数是 $m^{3}$

查看试题解析
17. 如图1，课本中有一道例题：有一块三角形余料 $A B C$ ，它的边 $B C = 120 m m$ ，高 $A D = 80 m m$ ．要把它加工成正方形零件，使正方形的一边在 $B C$ 上，其余两个顶点分别在 $A B$ ， $A C$ 上．设 $P N = x m m$ ，用 $x$ 的代数式表示 $A E =$ $m m$ ，由 $P N // B C$ ，可得 $△ A P N ∽ △ A B C$ ，再利用相似三角形对应高的比等于相似比，可求得 $P N =$ $m m$ ．

拓展：原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图2，此时， $P N =$ $m m$ ．

查看试题解析

三、解答题

18. 在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $B C = 3$ ， $A B = 5$ ，

(1)、求 $A C$ ；

(2)、求 $\tan A$ ．

查看试题解析
19. 科学研究发现．地表以下岩层的温度y（℃）与所处深度x（千米）之间近似地满足一次函数关系．经测量，在深度2千米的地方，岩层温度为 $90 ℃$ ；在深度5千米的地方，岩层温度为 $195 ℃$ ．

(1)、求出y与x的函数表达式；

(2)、求当岩层温达到 $1805 ℃$ 时，岩层所处的深度．

查看试题解析
20. 某数学课外小组，开展数学“闯关”游戏（游戏一共10关），根据活动结果，制成如下两幅尚不完整的统计图．

(1)、数学课外活动小组的总人数为； $a =$ ，请补充完整条形统计图；

(2)、求数学课外活动小组的平均闯关次数；

(3)、再新加入n名同学闯关，已知这n名同学的闯关次数均大于7，若加入后闯关次数的中位数与原闯关次数的中位数相等，求n的最大值．

查看试题解析
21. 如图，在矩形ABCD得对角线AC，BD交于点O，延长CD到点E，使 $D E = C D$ ，连接AE．

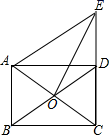(1)、求证：四边形ABDE是平行四边形；

(2)、连接OE，若 $A D = 4$ ， $A B = 2$ ，求OE的长．

查看试题解析
22. 直线 $y = - x - 2$ 与x轴相交于A点，与y轴相交于B点，直线 $y = k x + 2 - 4 k (k > 0)$ 与直线 $y = - x - 2$ 相交于C点．

(1)、请说明 $y = k x + 2 - 4 k (k > 0)$ 经过点（4，2）；

(2)、 $k = 1$ 时，点D是直线 $y = k x + 2 - 4 k (k > 0)$ 上一点且在y轴的右侧，若 $S_{△ D O B} = 2 S_{△ D O A}$ ，求点D的坐标；

(3)、若点C在第三象限，求k的取值范围．

查看试题解析
23. 对于代数式ax²+bx+c ，若存在实数n ，当x＝n时，代数式的值也等于n ，则称n为这个代数式的不变值．例如：对于代数式x² ，当x＝0时，代数式等于0；当x＝1时，代数式等于1，我们就称0和1都是这个代数式的不变值．在代数式存在不变值时，该代数式的最大不变值与最小不变值的差记作A ．特别地，当代数式只有一个不变值时，则A＝0．

(1)、代数式x²﹣2的不变值是， A＝．

(2)、说明代数式3x²+1没有不变值；

(3)、已知代数式x²﹣bx+1，若A＝0，求b的值．

查看试题解析
24. 如图1，在 $△ A B C$ 中， $A B = A C = 10$ ， $\tan B = \frac{3}{4}$ ，点D为 $B C$ 边上的动点（点D不与点B，C重合）．以D为顶点作 $∠ A D E = ∠ B$ ，射线 $D E$ 交 $A C$ 边于点E，过点A作 $A F ⊥ A D$ 交射线 $D E$ 于点F，连接 $C F$ ．

(1)、求证： $△ A B D ∽ △ D C E$ ；

(2)、当 $D E // A B$ 时（如图2），求 $A E$ 的长；

(3)、点D在 $B C$ 边上运动的过程中，当 $△ A E F$ 是等腰三角形时，直接写出 $B D$ 的长．

查看试题解析

	听	说	读	写
张明	90	80	83	82

月用水量 $(m^{3})$	$4$	$5$	$6$	$8$	$9$
户数	$4$	$6$	$5$	$4$	$1$