初中数学浙教版九年级下册第一章 解直角三角形 单元测试
试卷更新日期:2021-02-01 类型:单元试卷
一、单选题
-
1. 如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值( )A、扩大为原来的两倍 B、缩小为原来的 C、不变 D、不能确定2. 在Rt△ABC中,∠C=90°,若 ,则 的值为( )A、1 B、 C、 D、3. 已知A为锐角,且cosA≤ ,那么( )A、 B、 C、 D、4. 如下图要测量小河两岸相对的两点P、A的距离,可以在小河边取 的垂线 上的一点C,测得 米, ,则小河宽 为( )
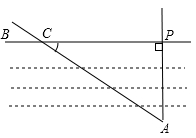 A、 米 B、 米 C、 米 D、 米5. 一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是( )
A、 米 B、 米 C、 米 D、 米5. 一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是( )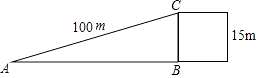 A、
A、 B、
B、 C、
C、 D、
D、 6. 在Rt△ABC中,∠C=90°,下列式子中不一定成立的是( )A、tanA= B、sin2A+sin2B=1 C、sin2A+cos2A=1 D、sinA=sinB7. 如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离(BC的长)为( )
6. 在Rt△ABC中,∠C=90°,下列式子中不一定成立的是( )A、tanA= B、sin2A+sin2B=1 C、sin2A+cos2A=1 D、sinA=sinB7. 如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离(BC的长)为( )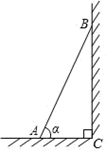 A、 米 B、 米 C、 米 D、 米8. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
A、 米 B、 米 C、 米 D、 米8. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.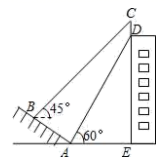 A、15-5 B、20-10 C、10-5 D、5 -59. 如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于( )
A、15-5 B、20-10 C、10-5 D、5 -59. 如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于( )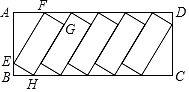 A、( a+ b)米 B、( a+ b)米 C、(a+ b)米 D、(a+ b)米10. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )
A、( a+ b)米 B、( a+ b)米 C、(a+ b)米 D、(a+ b)米10. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )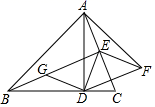 A、8 B、 C、 D、
A、8 B、 C、 D、二、填空题
-
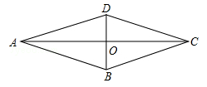
11. 在 中, 为直角, 、∠B、∠C所对的边分别为a、B、c,且 , ,则tan∠B = .12. 如图,菱形ABCD的对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是.
 13. 如图,渔船在 处看到灯塔 在北偏东 方向上,渔船向正东方向航行了 到达 处,在 处看到灯塔 在正北方向上,则 处与灯塔 的距离是 .
13. 如图,渔船在 处看到灯塔 在北偏东 方向上,渔船向正东方向航行了 到达 处,在 处看到灯塔 在正北方向上,则 处与灯塔 的距离是 .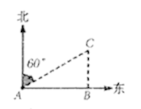 14. 如图,在△ABC中,∠A=30°,tanB= ,AC=2 ,AB的长 .
14. 如图,在△ABC中,∠A=30°,tanB= ,AC=2 ,AB的长 . 15. 一座建于若干年前的水库大坝的横截面如图所示,目前坝高4米,现要在不改变坝高的情况下修整加固,将背水坡AB的坡度由1:0.75改为1:2,则修整后的大坝横截面积增加了平方米.
15. 一座建于若干年前的水库大坝的横截面如图所示,目前坝高4米,现要在不改变坝高的情况下修整加固,将背水坡AB的坡度由1:0.75改为1:2,则修整后的大坝横截面积增加了平方米. 16. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
16. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .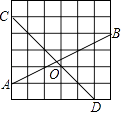
三、综合题
-
17. 计算:2cos245°+tan60°•tan30°﹣cos60°18. 在△ABC中,∠B=135°,AB= ,BC=1.
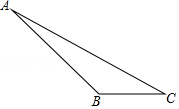 (1)、求△ABC的面积;(2)、求AC的长.19. 如图,一根电线杆PQ直立在山坡上,从地面的点A看,测得杆顶端点P的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和30°,求电线杆PQ的高度.(结果保留根号).
(1)、求△ABC的面积;(2)、求AC的长.19. 如图,一根电线杆PQ直立在山坡上,从地面的点A看,测得杆顶端点P的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和30°,求电线杆PQ的高度.(结果保留根号).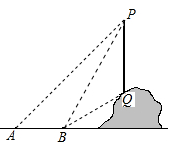 20.(1)、已知Rt△ABC中,∠C=90°,∠A=30°,BC= ,解直角三角形.(2)、已知△ABC中,∠A=45°,AB=4,BC=3,求AC的长.21. 如图是一种简易台灯的结构图,灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
20.(1)、已知Rt△ABC中,∠C=90°,∠A=30°,BC= ,解直角三角形.(2)、已知△ABC中,∠A=45°,AB=4,BC=3,求AC的长.21. 如图是一种简易台灯的结构图,灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.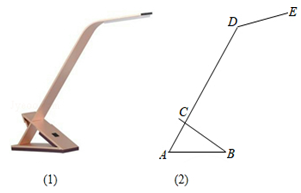 (1)、求DE与水平桌面(AB所在直线)所成的角;(2)、当E点到水平桌面(AB所在直线)的距离介于45cm至46cm范围时,视线最佳,通过计算说明此时光线是否为最佳.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27, =1.73.)22. 某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示, ,斜坡 长为 ,坡度 .为了减缓坡面,防止山体滑坡,保障安全,学校决定对该斜坡进行改造,地质人员勘测,当坡角不超过 时,可确保山体不滑坡.
(1)、求DE与水平桌面(AB所在直线)所成的角;(2)、当E点到水平桌面(AB所在直线)的距离介于45cm至46cm范围时,视线最佳,通过计算说明此时光线是否为最佳.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27, =1.73.)22. 某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示, ,斜坡 长为 ,坡度 .为了减缓坡面,防止山体滑坡,保障安全,学校决定对该斜坡进行改造,地质人员勘测,当坡角不超过 时,可确保山体不滑坡. (1)、求改造前坡顶到地面的距离 .(2)、如果改造时保持坡脚 不动,坡顶 沿 削进到 处,问 至少是多少米?23. 一轮船以每小时30km的速度由西向东航行(如图),在途中C处接到台风警报,台风中心正以每小时20km的速度从B处由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.
(1)、求改造前坡顶到地面的距离 .(2)、如果改造时保持坡脚 不动,坡顶 沿 削进到 处,问 至少是多少米?23. 一轮船以每小时30km的速度由西向东航行(如图),在途中C处接到台风警报,台风中心正以每小时20km的速度从B处由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.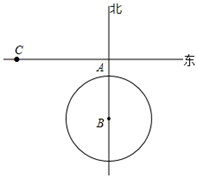 (1)、如果轮船不改变航向,轮船会不会进入台风影响区?若不会受到影响,说明理由;若会受到影响,求出受影响的时间(结果保留整数).(2)、现轮船速度减慢为每小时vkm(v<30),航向不变,在保证不受到台风影响的前提下,求v的最大值(结果保留整数).24. 如图1,已知矩形ABCD中,AB=6,BC=8,O是对角线AC的中点,点E从A点沿AB向点B运动,运动过程中连接OE,过O作OF⊥OE交BC于F,连接EF,
(1)、如果轮船不改变航向,轮船会不会进入台风影响区?若不会受到影响,说明理由;若会受到影响,求出受影响的时间(结果保留整数).(2)、现轮船速度减慢为每小时vkm(v<30),航向不变,在保证不受到台风影响的前提下,求v的最大值(结果保留整数).24. 如图1,已知矩形ABCD中,AB=6,BC=8,O是对角线AC的中点,点E从A点沿AB向点B运动,运动过程中连接OE,过O作OF⊥OE交BC于F,连接EF,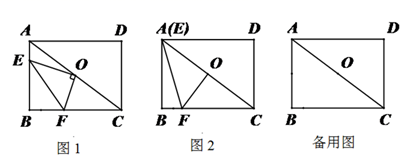 (1)、当点E与点A重合时,如图2,求 的值;(2)、运动过程中, 的值是否与(1)中所求的值保持不变,并说明理由;(3)、当EF平分∠OEB时,求AE的长.
(1)、当点E与点A重合时,如图2,求 的值;(2)、运动过程中, 的值是否与(1)中所求的值保持不变,并说明理由;(3)、当EF平分∠OEB时,求AE的长.