黑龙江省哈尔滨市南岗区“FF联盟”2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-02-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个方程中，是一元一次方程的是（）

A、 $x + 3 = y - 6$ B、 $x^{2} = 4$ C、 $\frac{5}{x} = 1$ D、 $x + 2 = 2 - x$

查看试题解析
2. 如图为一只小兔，将图进行平移，得到的图形可能是下列选项中的（）

A、 B、 C、 D、

查看试题解析
3. 下列等式变形正确的是（）

A、如果 $x - 3 = y - 3$ ，那么 $x - y = 0$ B、如果 $x + 1 = y - 1$ ，那么 $x + 2 = y - 2$ C、如果 $m x = m y$ ，那么 $x = y$ D、如果 $\frac{1}{2} x = 6$ ，那么 $x = 3$

查看试题解析
4. 如果x=2是方程 $\frac{1}{2}$ x+a=﹣1的解，那么a的值是（）

A、0 B、2 C、﹣2 D、﹣6

查看试题解析
5. 在同一平面内，不重合的三条直线a、b、c中，如果 $a ⊥ b$ ， $b ⊥ c$ ，那么a与c的位置关系是（）

A、垂直 B、平行 C、相交 D、不能确定

查看试题解析
6. 下列所示的四个图形中，∠1和∠2是同位角的是（）

A、②③ B、①②③ C、①②④ D、①④

查看试题解析
7. 下列方程变形中，正确的是（）

A、方程 $5 x - 2 = 2 x + 1$ ，移项，得 $5 x - 2 x = - 1 + 2$ B、方程 $3 - x = 2 - 5 (x - 1)$ ，去括号，得 $3 - x = 2 - 5 x + 1$ C、方程 $\frac{4}{3} x = \frac{3}{4}$ ，系数化为1，得 $x = 1$ D、方程 $\frac{x + 1}{5} = \frac{3 x - 1}{5} - 1$ ，去分母得 $x + 1 = 3 x - 1 - 5$

查看试题解析
8. 船在静水中的速度为36千米/时，水流速度为4千米/时，从甲码头到乙码头再返回甲码头，共用了9小时（中途不停留），设甲、乙两码头的距离为 $x$ 千米，则下面所列方程正确的是（）

A、 $(36 + 4) x + (36 - 4) (9 - x) = 1$ B、 $(36 + 4) x = 9$ C、 $\frac{x}{36} + \frac{x}{4} = 9$ D、 $\frac{x}{36 + 4} + \frac{x}{36 - 4} = 9$

查看试题解析
9. 两件商品都卖84元，其中一件亏本20%，另一件赢利40%，则两件商品卖后（）

A、赢利16.8元 B、亏本3元 C、赢利3元 D、不赢不亏

查看试题解析
10. 下列说法正确的是（）
①在同一平面内，过一点有且只有一条直线与已知直线垂直；

②在同一平面内，过一点有且只有一条直线与已知直线平行；

③ $P$ 是直线 $a$ 外一点， $A$ 、 $B$ 、 $C$ 分别是直线 $a$ 上的三点， $P A = 1$ ， $P B = 2$ ， $P C = 3$ ，则点 $P$ 到直线 $a$ 的距离一定是1；

④相等的角是对顶角；

⑤同旁内角互补．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知方程 $2 x^{m}^{+ 1} + 3 = 0$ 是关于 $x$ 的一元一次方程，则 $m$ 的值是．

查看试题解析
12. 当x=时，代数式 $4 x - 5$ 的值等于7．

查看试题解析
13. 兄弟二人今年分别为15岁和5岁，年后兄的年龄是弟的年龄的2倍．

查看试题解析
14. 已知∠1与∠2是对顶角，∠2与∠3是邻补角，则∠1+∠3= ．

查看试题解析
15. 把命题“对顶角相等”改写成“如果…那么…”的形式是.

查看试题解析
16. 如图，将 $△ A B C$ 沿水平方向向右平移到 $△ D E F$ 的位置，已知点 $A$ 、点 $D$ 之间的距离为5， $C E = 7$ ，则 $B F$ 的长为．

查看试题解析
17. 如图，已知AB∥CD，BE平分∠ABC，∠CDE=150°，则∠C=°．

查看试题解析
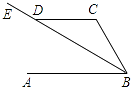18. 2004年中国足球甲级联赛规定每队胜一场得3分、平一场得1分、负一场得0分，武汉黄鹤楼队前14场保持不败，共得30分该队共平了场．

查看试题解析
19. 已知直线AB和CD相交于O点，射线OE⊥CD于O ，且∠BOE＝25°．则∠AOC的度数为．

查看试题解析
20. 如图， $A B // C D$ ， $∠ A C D = 60 °$ ， $∠ B A E ： ∠ C A E = 2 ： 3$ ， $∠ F C D = 4 ∠ F C E$ ，若 $∠ A E C = 78 °$ ，则 $∠ F C E =$ ．

查看试题解析

三、解答题

21. 解方程

(1)、 $2 (2 x - 5) - (5 x + 3) = 4$

(2)、 $\frac{2 x - 1}{3} = \frac{3 x + 5}{2} - 1$

查看试题解析
22. 如图，网格中每个小正方形的边长为1个单位长度，三角形 $A B C$ 中，点 $A$ 、点 $B$ 、点 $C$ 均在格点上．

(1)、在图1中，过点 $C$ 画出线段 $A B$ 的垂线；

(2)、在图1中，过点 $B$ 画出直线 $B M$ ，使 $B M // A C$ ；

(3)、在图2中，先将三角形 $A B C$ 向右平移5个单位长度，再向上平移4个单位长度，得到三角形 $A_{1} B_{1} C_{1}$ ，画出三角形 $A_{1} B_{1} C_{1}$ ．

查看试题解析
23. 整理一批图书，由一个人做要40小时完成.现计划由一部分人先做4小时，再增加2人和他们一起做8小时，完成这项工作.假设这些人的工作效率相同，具体应先安排多少人工作？

查看试题解析
24. 在下面的括号内，填上推理的根据．
已知：如图，∠1=∠2，∠4+∠5=180°，求证：∠6=∠7．

证明∵∠1=∠2

∠2=∠3（     ▲    ）

∴∠1=∠3

∴ $a // c$

∵∠4+∠5=180°

∴ $b // c$ （     ▲    ）

∴ $a // b$ （     ▲    ）

∴∠6=∠7（     ▲    ）

查看试题解析
25. 在三角形 $A B C$ 中， $C D ⊥ A B$ 于点 $D$ ， $F$ 是 $B C$ 上一点， $F H ⊥ A B$ 于点 $H$ ，点 $E$ 在 $A C$ 上， $∠ E D C = ∠ B F H$ ．

(1)、如图1，求证： $D E // B C$ ；

(2)、如图2，延长 $E D$ 、 $F H$ 交于点 $G$ ，若 $∠ A C B = 90 °$ ，请直接写出图中与 $∠ B$ 互余的角，不需要证明．

查看试题解析
26. 某商场从厂家购进了 $A$ 、 $B$ 两种品牌足球共100个已知购买 $A$ 品牌足球比购买 $B$ 品牌足球少花2800元，其中 $A$ 品牌足球每个进价是50元， $B$ 品牌足球每个进价是80元．

(1)、求购进 $A$ 、 $B$ 两种品牌足球各多少个？

(2)、在销售过程中， $A$ 品牌足球每个售价是80元很快全部售出； $B$ 品牌足球每个按进价加价25％销售，售出一部分后，出现滞销，商场决定打九折出售剩余的 $B$ 品牌足球，两种品牌足球全部售出后共获利2200元，有多少个 $B$ 品牌足球打九折出售？

查看试题解析
27. 已知， $A E // B D$ ， $∠ A = ∠ D$ ．

(1)、如图1，求证： $A B // C D$

(2)、如图2，作 $∠ B A E$ 的平分线交 $C D$ 于点 $F$ ，点 $G$ 为 $A B$ 上一点，连接 $F G$ ，若 $∠ C F G$ 的平分线交线段 $A G$ 于点 $H$ ，求证： $∠ E C F + 2 ∠ A F H = ∠ E + 2 ∠ B H F$ ；

(3)、如图3，在（2）的条件下，连接 $A C$ ，若 $∠ A C E = ∠ B A C + ∠ B G M$ ，过点 $H$ 作 $H M ⊥ F H$ 交 $F G$ 的延长线于点 $M$ ，且 $2 ∠ E - 3 ∠ A F H = 20 °$ ，求 $∠ E A F + ∠ G M H$ 的度数．

查看试题解析