黑龙江省哈尔滨市通河县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-02-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列为一元二次方程的是（）

A、 $x + \frac{1}{x} = 1$ B、 $x^{2} + 2 x + 1$ C、 $x (x + 1) = 4$ D、 $x^{2} + y + 6 = 0$

查看试题解析
2. 在抛物线y=-x²+1 上的一个点是( )．

A、(1，0) B、(0，0) C、（0，-1) D、（1，I)

查看试题解析
3. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 一元二次方程 $x^{2} - 4 x + 4 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
5. 抛物线 $y = 3 {(x - 1)}^{2} + 1$ 的顶点坐标是（）

A、 $(1, 1)$ B、 $(- 1, 1)$ C、 $(- 1, - 1)$ D、 $(1, - 1)$

查看试题解析
6. 将抛物线y＝5x²先向右平移3个单位，再向上平移2个单位后，所得的抛物线的解析式为（　　）

A、y＝5（x+3）²+2 B、y＝5（x+3）²﹣2 C、y＝5（x﹣3）²+2 D、y＝5（x﹣3）²﹣2

查看试题解析
7. 某工厂一月份生产零件50万个，由于引进新技术提高了生产效率，三月份的产量达到了72万个，设该厂二、三月份平均每月的增长率为x，那么x满足的方程是（）

A、 $50 (1 + 2 x) = 72$ B、 $50 + 50 (1 + x) = 72$ C、 $50 {(1 + x)}^{2} = 72$ D、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 72$

查看试题解析
8. 如图，把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C ， ∠A＝30°，∠1＝70°，则旋转角θ可能等于（　　）

A、40° B、50° C、70° D、100°

查看试题解析
9. 如图， $R t Δ O D C$ 的直角顶点D在y轴上， $D C$ 边上的点 $P (\sqrt{2} ， 2)$ 在抛物线 $y = a x^{2}$ 上，将 $R t Δ O D C$ 绕点O逆时针旋转 $90 °$ ，得到 $Δ O B A$ ，点A恰好在抛物线上，则点A的坐标为（）.

A、 $(- 2 ， 3)$ B、 $(- 2 ， 4)$ C、 $(- 2 ， 2 \sqrt{2})$ D、 $(- \sqrt{2} ， 2)$

查看试题解析
10. 二次函数y＝ax²＋bx＋c(a≠0)的图象如图所示，下列结论：①b＜0；②c＞0；③a＋c＜b；④b²－4ac＞0，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 在平面直角坐标系中，点P（5，3）关于原点对称的点的坐标为．

查看试题解析
12. 抛物线y＝（x﹣6）²﹣1的对称轴是直线．

查看试题解析
13. 已知方程x²﹣5x+15=k²的一个根是2，则另一个根是．

查看试题解析
14. 若抛物线 $y = a x^{2}$ 经过点（2，8），则a= ．

查看试题解析
15. 若二次函数 $y = a x^{2} + b x + a^{2} - 2$ （ $a$ 、 $b$ 为常数）的图象如图，则 $a$ 的值为

查看试题解析
16. 抛物线 $y = a x^{2} - 4 x + 3$ 过点A（2，3），则此抛物线开口向．

查看试题解析
17. 关于x的方程 $k x^{2} - 8 x + 8 = 0$ 有两个实数根，则k的取值范围．

查看试题解析
18. 三角形两边长分别为3和5，第三边满足方程x²-6x+8=0，则这个三角形的形状是．

查看试题解析
19. 在平面直角坐标系中，将点P（﹣3，2）绕点O（0，0）顺时针旋转90°，所得到的对应点P′的坐标为．

查看试题解析
20. 如图，△EDC是将△ABC绕点C顺时针旋转90°得到的．若点A，D，E在同一条直线上，则∠BAD的度数是．

查看试题解析

三、解答题

21. 用适当的方法解方程：

(1)、 ${(x + 3)}^{2} = 2 x + 6$

(2)、 $x^{2} - 8 x + 1 = 0$ ．

查看试题解析
22. △ABC在平面直角坐标系中如图：

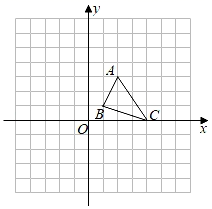(1)、画出将△ABC绕点O逆时针旋转90°所得到的△A₁B₁C₁ ，并写出A₁点的坐标；

(2)、画出△A₁B₁C₁关于原点成中心对称的△A₂B₂C₂ ，并直接写出△AA₁A₂的面积．

查看试题解析
23. 已知二次函数y=2x²+bx+1的图象过点（2，3）．

(1)、求该二次函数的表达式；

(2)、若点P（m ， m²+1）也在该二次函数的图象上，求点P的坐标．

查看试题解析
24. 如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，求FM的长．

查看试题解析
25. 工艺商场按标价销售某种工艺品时，每件可获利45元；并且进价50件工艺品与销售40件工艺品的价钱相同.

(1)、该工艺品每件的进价、标价分别是多少元？

(2)、若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件.若每件工艺品降价1元，则每天可多售出该工艺品4件.问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元?

查看试题解析
26. 已知抛物线y=-x²+4x+5．

(1)、用配方法将y=-x²+4x+5化成y=a（x﹣h）²+k的形式；

(2)、指出抛物线的开口方向、对称轴和顶点坐标；

(3)、若抛物线上有两点A（x₁ ， y₁），B(x₂ ， y₂)，如果x₁>x₂>2，试比较y₁与y₂的大小.

查看试题解析
27. 如图，在△AOB中，∠O＝90°，AO＝18cm，BO＝30cm，动点M从点A开始沿边AO以1cm/s的速度向终点O移动，动点N从点O开始沿边OB以2cm/s的速度向终点B移动，一个点到达终点时，另一个点也停止运动．如果M、N两点分别从A、O两点同时出发，设运动时间为ts时四边形ABNM的面积为Scm² ．

(1)、求S关于t的函数关系式，并直接写出t的取值范围；

(2)、判断S有最大值还是有最小值，用配方法求出这个值．

查看试题解析