广东省江门市恩平市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-02-01 类型:期中考试
一、单选题
-
1. 方程3x2﹣1=0的常数项是( )A、﹣1 B、0 C、3 D、12. 一元二次方程x2﹣2x+3=0的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、有两个实数根3. 一元二次方程 x2﹣2x﹣7=0 用配方法可变形为( )A、(x+1)2=8 B、(x+2)2=11 C、(x﹣1)2=8 D、(x﹣2)2=114. 一元二次方程x2+4x﹣3=0的两根为x1、x2 , 则x1·x2的值是( )A、4 B、﹣4 C、3 D、﹣35. 下列图案中不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( )
6. 如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( ) A、45° B、60° C、90° D、120°7. 把抛物线y=2x2先向左平移3个单位,再向上平移4个单位,所得抛物线的函数表达式为( )A、y=2(x+3)2+4 B、y=2(x+3)2﹣4 C、y=2(x﹣3)2﹣4 D、y=2(x﹣3)2+48. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A、45° B、60° C、90° D、120°7. 把抛物线y=2x2先向左平移3个单位,再向上平移4个单位,所得抛物线的函数表达式为( )A、y=2(x+3)2+4 B、y=2(x+3)2﹣4 C、y=2(x﹣3)2﹣4 D、y=2(x﹣3)2+48. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )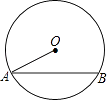 A、6 B、5 C、4 D、39. 如图,四边形ABCD内接于⊙O,E在BC延长线上,若∠DCE=50°,则∠A等于( )
A、6 B、5 C、4 D、39. 如图,四边形ABCD内接于⊙O,E在BC延长线上,若∠DCE=50°,则∠A等于( ) A、40° B、50° C、70° D、80°10. 函数y=ax2与y=﹣ax+b的图象可能是( )A、
A、40° B、50° C、70° D、80°10. 函数y=ax2与y=﹣ax+b的图象可能是( )A、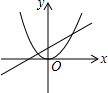 B、
B、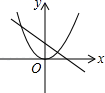 C、
C、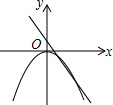 D、
D、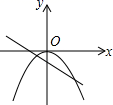
二、填空题
-
11. 将方程x(x﹣1)=3x+1化为一元二次方程的一般形式 .12. 点P(﹣3,﹣4)关于原点对称的点的坐标是 .13. 二次函数y=2(x﹣3)2﹣4的顶点是 .14. 某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=12m,半径OA=10m,则中间柱CD的高度为m.
 15. 已知⊙O的直径AB=8cm,C为⊙O上的一点,∠BAC=30°,则BC=cm.
15. 已知⊙O的直径AB=8cm,C为⊙O上的一点,∠BAC=30°,则BC=cm. 16. 如图,在⊙O中,∠BOC=100°,则∠A的度数是 .
16. 如图,在⊙O中,∠BOC=100°,则∠A的度数是 . 17. 已知二次函数的y=ax2+bx+c (a≠0)图象如图所示,有下列4个结论:①abc<0;②b<a+c;③2a+b=0;④a+b<m (am+b) (m≠1的实数),其中正确的结论有 .
17. 已知二次函数的y=ax2+bx+c (a≠0)图象如图所示,有下列4个结论:①abc<0;②b<a+c;③2a+b=0;④a+b<m (am+b) (m≠1的实数),其中正确的结论有 .
三、解答题
-
18. 解方程:x2﹣4x﹣12=0.19. 已知抛物线的顶点坐标是(2,1),且该抛物线经过点A(3,3),求该抛物线解析式.20. 已知关于x的一元二次方程x2﹣mx+12=0的一根为x=﹣3,求m的值以及方程的另一根.21. 如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°得到,且AB⊥BC , 连接DE .
 (1)、∠DBE的度数.(2)、求证:△BDE≌△BCE .22. 已知抛物线y=x2+4x﹣5;(1)、求出该抛物线的开口方向、对称轴和顶点坐标;(2)、求该抛物线与x轴、y轴的交点坐标.23. 随着经济的发展,李进所在的公司每年都在元月一次性的提高员工当年的月工资.李进2009年的月工资为2000 元,在2011年时他的月工资增加到2420元.(1)、求2009到2011年的月工资的平均增长率.(2)、若他2012年的月工资按相同的平均增长率继续增长,李进2012年的月工资是多少元?24. 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)、∠DBE的度数.(2)、求证:△BDE≌△BCE .22. 已知抛物线y=x2+4x﹣5;(1)、求出该抛物线的开口方向、对称轴和顶点坐标;(2)、求该抛物线与x轴、y轴的交点坐标.23. 随着经济的发展,李进所在的公司每年都在元月一次性的提高员工当年的月工资.李进2009年的月工资为2000 元,在2011年时他的月工资增加到2420元.(1)、求2009到2011年的月工资的平均增长率.(2)、若他2012年的月工资按相同的平均增长率继续增长,李进2012年的月工资是多少元?24. 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE. (1)、求证:∠B=∠D;(2)、若AB=10,BC﹣AC=2,求CE的长.25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)、求证:∠B=∠D;(2)、若AB=10,BC﹣AC=2,求CE的长.25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C. (1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.