吉林省长春市宽城区2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-02-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $x^{3} + x^{3} = 2 x^{6}$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 $x^{6} \div x^{3} = x^{3}$ D、 ${(- 2 x)}^{3} = - 6 x^{3}$

查看试题解析
2. 把多项式a²－4a分解因式，结果正确的是（）

A、a (a-4) B、(a+2)(a-2) C、a(a+2)( a-2) D、(a－2 ) ²－4

查看试题解析
3. 下列命题中，是假命题的是（）

A、两条直角边对应相等的两个直角三角形全等 B、两个锐角对应相等的两个直角三角形全等 C、斜边和一条直角边对应相等的两个直角三角形全等 D、斜边和一个锐角对应相等的两个直角三角形全等

查看试题解析
4. 若 $a > 0$ ， $a^{x} = 2$ ， $a^{y} = 3$ ，则 $a^{x - 2 y}$ 的值为（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
5. 如图， $△ A B C ≌ △ A D E$ ，点 $D$ 在边 $B C$ 上，则下列结论中一定成立的是（）

A、 $A C = D E$ B、 $A B = B D$ C、 $∠ A B D = ∠ A D B$ D、 $∠ E D C = ∠ A E D$

查看试题解析
6. 如图，在 $△ A B C$ 与 $△ A D C$ 中， $A B = A D$ ， $C B = C D$ ．若 $∠ B = 118 °$ ，则 $∠ B A C + ∠ A C D$ 的度数为（）

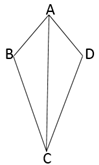A、52 ° B、62° C、72° D、118°

查看试题解析
7. 如图，等腰△ $A B C$ 中，点D ， E分别在腰AB ， AC上，添加下列条件，不能判定 $△ A B E$ ≌ $△ A C D$ 的是（）

A、 $A D = A E$ B、 $B E = C D$ C、 $∠ A D C = ∠ A E B$ D、 $∠ D C B = ∠ E B C$

查看试题解析
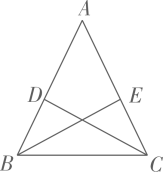8. 图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是

A、 B、 ${(a + b)}^{2}$ C、 D、

查看试题解析

二、填空题

9. 计算： ${(- a^{3})}^{2} =$ ．

查看试题解析
10. 分解因式： $x^{2} - x - 12$ =.

查看试题解析
11. 命题“如果 $a = b$ ，那么 $a^{2} = b^{2}$ ”是命题．（填“真”或“假”）

查看试题解析
12. 若 $(x - 3) (2 x + m)$ 的计算结果中不含 $x$ 的一次项，则 $m$ 的值是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ B = ∠ C = 40 °$ ，点 $D$ 在边 $B C$ 上，且 $∠ D A C = 50 °$ ．若 $B D = 5$ ，则 $B C$ 的长为．

查看试题解析
14. 如图，在 $△ A B C$ 与 $△ A E F$ 中，AB、EF相交于点D，点F在边BC上， $A B = A E$ ， $B C = E F$ ， $∠ B = ∠ E$ ．下列结论：① $∠ E A B = ∠ A F C$ ；② $∠ A F E = ∠ A F C$ ；③ $∠ B F E = ∠ A F C$ 中，正确的是．（填序号）

查看试题解析

三、解答题

15. 把下列多项式分解因式：

(1)、 $2 x^{2} - 4 x + 2$

(2)、 $12 a^{2} - 3 b^{2}$

查看试题解析
16. 计算： $(x + y) (x - y) - (4 x^{3} y - 4 x y^{3}) \div (2 x y)$

查看试题解析
17. 图①、图②均是正方形网格，每个小正方形的顶点称为格点， $△ P Q R$ 的顶点及点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 均在格点上，在图①、图②中，按要求各画一个与 $△ P Q R$ 全等的三角形要求：

①两个三角形分别以 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 中的三个点为顶点；

②两个三角形的顶点不完全相同．

查看试题解析
18. 先化简，再求值： $(2 m + 3) (2 m - 3) - {(m + 2)}^{2} + 4 (m + 3)$ ，其中 $m = - \frac{1}{3}$ ．

查看试题解析
19. 如图，在 $Δ A B C$ 与 $△ C D E$ 中，点 $C$ 在线段 $B D$ 上，且 $A B ⊥ B D$ ， $D E ⊥ B D$ ， $A C = C E$ ， $B C = D E$ ．

(1)、求证： $A B = C D$ ．

(2)、求 $∠ A C E$ 的度数．

查看试题解析
20. 小刚同学计算一道整式乘法： $(2 x + a) (3 x - 2)$ ，由于他抄错了多项式中 $a$ 前面的符号，把“+”写成“一”，得到的结果为 $6 x^{2} + b x + 10$ ．

(1)、求 $a$ 、 $b$ 的值．

(2)、计算这道整式乘法的符合题意结果．

查看试题解析
21. 如图，将一张大长方形纸板按图中虚线裁剪成9块，其中有2块是边长为a厘米的大正方形，2块是边长都为b厘米的小正方形，5块是长为a厘米，宽为b厘米的相同的小长方形，且a＞b．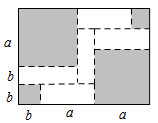

(1)、观察图形，可以发现代数式2a²+5ab+2b²可以因式分解为.

(2)、若图中阴影部分的面积为242平方厘米，大长方形纸板的周长为78厘米，求图中空白部分的面积.

查看试题解析
22. 如图， $△ A B C$ 是等边三角形，点 $D$ 、 $E$ 分别在边 $B C$ 、 $A C$ 上，且 $A E = C D$ ， $A D$ 与 $B E$ 相交于点 $P$ ， $B Q ⊥ A D$ 于点 $Q$ ．

(1)、求证： $△ A B E ≌ △ C A D$ ．

(2)、求 $∠ P B Q$ 的度数．

查看试题解析
23. 按要求解答

(1)、你能求出（a﹣1）（a⁹⁹+a⁹⁸+a⁹⁷+…+a²+a+1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．
（a﹣1）（a+1）；（a﹣1）（a²+a+1）；（a﹣1）（a³+a²+a+1）；…

由此我们可以得到：（a﹣1）（a⁹⁹+a⁹⁸+…+a+1）的值．

(2)、利用（1）的结论，完成下面的计算：
2¹⁹⁹+2¹⁹⁸+2¹⁹⁷+…+2²+2+1．

查看试题解析
24. $C D$ 是经过 $∠ A C B$ 顶点 $C$ 的一条直线， $C A = C B$ ． $E$ 、 $F$ 分别是直线 $C D$ 上两点，点 $E$ 在点 $F$ 的左侧，且 $∠ B E C = ∠ C F A = ∠ α$ ．

(1)、直线 $C D$ 经过 $∠ A C B$ 的内部， $E$ 、 $F$ 两点在射线 $C D$ 上．如图1，若 $∠ A C B = 90 °$ ， $∠ α = 90 °$ ，则 $B E$ $C F$ （填“ $>$ ”、“ $<$ ”或“ $=$ ”）； $E F$ 、 $B E$ 、 $A F$ 三条线段之间的数量关系是：．

(2)、如图2，若 $0 ° < ∠ A C B < 180 °$ ， $∠ α + ∠ A C B = 180 °$ ，（1）中的两个结论是否仍然成立，请说明理由．

(3)、如图3，若直线 $C D$ 经过 $∠ A C B$ 的外部， $∠ α = ∠ A C B$ ，请直接写出 $E F$ 、 $B E$ 、 $A F$ 三条线段之间的数量关系．

查看试题解析