黑龙江省绥化市肇东市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-02-01 类型:期中考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 在Rt△ABC中, ,则AB的长是( )A、 B、2 C、1 D、3. 下列计算正确的是( )A、 - = B、 ÷ = C、3 +2 =5 D、 = ×4. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线互相垂直 D、正方形的对角线相等5. 如图,▱ABCD中,EF过对角线的交点O,AB=5,AD=3,OF=1.2,则四边形BCEF的周长为( )
 A、9.2 B、9.4 C、10.4 D、13.46. 在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中错误的是( )A、如果∠A﹣∠B=∠C,那么△ABC 是直角三角形 B、如果∠A:∠B:∠C=1:2:3,那么△ABC 是直角三角形 C、如果 a2:b2:c2=9:16:25,那么△ABC 是直角三角形 D、如果 a2=b2﹣c2 , 那么△ABC 是直角三角形且∠A=90°7. 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A、9.2 B、9.4 C、10.4 D、13.46. 在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中错误的是( )A、如果∠A﹣∠B=∠C,那么△ABC 是直角三角形 B、如果∠A:∠B:∠C=1:2:3,那么△ABC 是直角三角形 C、如果 a2:b2:c2=9:16:25,那么△ABC 是直角三角形 D、如果 a2=b2﹣c2 , 那么△ABC 是直角三角形且∠A=90°7. 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( ) A、60° B、45° C、30° D、75°8. 平行四边形 中,若 ,则 的度数为( ).A、 B、 C、 D、9. 如图,▱ABCD的对角线 交于点 ,且AC: :3,那么AC的长为( )
A、60° B、45° C、30° D、75°8. 平行四边形 中,若 ,则 的度数为( ).A、 B、 C、 D、9. 如图,▱ABCD的对角线 交于点 ,且AC: :3,那么AC的长为( ) A、 B、 C、3 D、410. 如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是( )
A、 B、 C、3 D、410. 如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是( ) A、36 B、45 C、54 D、64
A、36 B、45 C、54 D、64二、填空题
-
11. 把 化为最简二次根式,结果是.12. 最简二次根式 与 是同类二次根式,则b= .13. 若a、b、c满足(a-5)2+ + =0,则以a,b,c为边的三角形面积是.14. 如图,在平行四边形ABCD中,DE平分∠ADC,AD=7,BE=2,则平行四边形ABCD的周长是 .
 15. 如图,在平面直角坐标系xOy中,已知点A( ,0),B(1,1).若平移点B到点D,使四边形OADB是平行四边形,则点D的坐标是.
15. 如图,在平面直角坐标系xOy中,已知点A( ,0),B(1,1).若平移点B到点D,使四边形OADB是平行四边形,则点D的坐标是. 16. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=54°,则∠AEG= .
16. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=54°,则∠AEG= . 17. 实数a、b在数轴上的位置如图所示,则化简 的结果为 .
17. 实数a、b在数轴上的位置如图所示,则化简 的结果为 . 18. 在△ABC中,AB=15,AC=13,高AD=12,则 的周长为 .19. 如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF= .
18. 在△ABC中,AB=15,AC=13,高AD=12,则 的周长为 .19. 如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF= . 20. 如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为 .
20. 如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为 .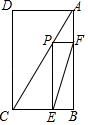 21. 如图,平行四边形纸片 中, ,将平行四边形纸片 折叠,使点A与点C重合,则下列结论正确的是.
21. 如图,平行四边形纸片 中, ,将平行四边形纸片 折叠,使点A与点C重合,则下列结论正确的是.① ;② ;③ ;④
三、解答题
-
22. 计算:(1)、 ﹣4 + ÷ ;(2)、(1﹣ )(1+ )+(1+ )2 .23. 如图,在平行四边形ABCD中,AE=CF,求证:四边形BFDE是平行四边形.
 24. 如图是一块地,已知AD=4,CD=3,AB=13,BC=12,且CD⊥AD,求这块地的面积.
24. 如图是一块地,已知AD=4,CD=3,AB=13,BC=12,且CD⊥AD,求这块地的面积. 25. 阅读理解:把分母中的根号化去叫做分母有理化,例如:① = = ;② = = = .等运算都是分母有理化,根据上述材料,(1)、化简: ;(2)、 + + +…+ .26. 如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.求证:OM=ON.
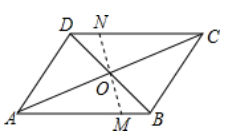
25. 阅读理解:把分母中的根号化去叫做分母有理化,例如:① = = ;② = = = .等运算都是分母有理化,根据上述材料,(1)、化简: ;(2)、 + + +…+ .26. 如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.求证:OM=ON. 27. 如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.求证:四边形ABEF是菱形;
27. 如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.求证:四边形ABEF是菱形;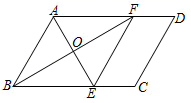 28. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
28. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. (1)、求证:CE=CF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?29. 已知点O是△ABC内任意一点,连接OA并延长到点E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC,连接OF,与BC交于点H,连接EF.(1)、问题发现:如图1,若△ABC为等边三角形,线段EF与BC的位置关系是 , 数量关系为;
(1)、求证:CE=CF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?29. 已知点O是△ABC内任意一点,连接OA并延长到点E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC,连接OF,与BC交于点H,连接EF.(1)、问题发现:如图1,若△ABC为等边三角形,线段EF与BC的位置关系是 , 数量关系为; (2)、拓展探究:如图2,若△ABC为等腰直角三角形(BC为斜边),(1)中的两个结论是否成立?若成立,请给予证明;若不成立,请写出正确的结论再给予证明;
(2)、拓展探究:如图2,若△ABC为等腰直角三角形(BC为斜边),(1)中的两个结论是否成立?若成立,请给予证明;若不成立,请写出正确的结论再给予证明; (3)、解决问题:如图3,若△ABC是等腰三角形,AB=AC=5,BC=6,请你直接写出线段EF的长.
(3)、解决问题:如图3,若△ABC是等腰三角形,AB=AC=5,BC=6,请你直接写出线段EF的长.