黑龙江省齐齐哈尔市建华区2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2021-02-01 类型：期中考试
一、单选题
-
1. 中国文字博大精深，而且有许多是轴对称图形，在这四个文字中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列各组线段为边，能组成三角形的是（ ）A、2，3，5 B、2，3，6 C、8，6，4 D、6，7，143. 下列说法：①已知△ABC中，AB＝6，AC＝8，则中线AD的取值范围是1≤AD≤7；
②两边和一角对应相等的两个三角形全等；
③如果两个三角形关于某直线成轴对称，那么它们是全等三角形；
④一腰上的中线也是这条腰上的高的等腰三角形是等边三角形．
其中正确的有（ ）
A、1个 B、2个 C、3 D、4个4. 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（ ）A、7 B、7或8 C、8或9 D、7或8或95. 在直角坐标系中，已知A（-3，3），在y轴上确定一点P ， 使△AOP为等腰三角形，则符合条件的点P共有（ ）A、2个 B、3个 C、4个 D、5个6. 如图，AD，AE分别为△ABC的高线和角平分线，DF⊥AE于点F，当∠ADF＝69°，∠C＝65°时，∠B的度数为（ ）
A、21° B、23° C、25° D、30°7. 已知线段a、b、c分别为三角形的三边长，则化简|a+c-b|-|c-a-b|的结果为（ ）A、2c-2b B、2b-2c C、-2a D、2a8. 如图，把△ 沿 对折，叠合后的图形如图所示.若 ， ，则∠2的度数为（ ）
A、24° B、35° C、30° D、25°9.如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）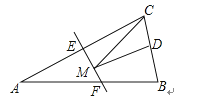
A、6 B、8 C、10 D、1210. 如图，已知△ABC中，AB＝6，BC＝5，AC＝4，∠ABC，∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，连AF，则下列结论：①DE＝BD+CE；②∠BFC＝90°+ ∠ABC；③△ADE的周长为10；④S△ABF：S△ACF：S△BCF＝6：4：5．正确的是（ ）
A、①③④ B、①②③ C、①②③④ D、②③④二、填空题
-
11. 知P1（a-1，4）和P2（2，b）关于x轴对称，则（a+b）2021的值为 ．12. 如图，点D，E分别在线段AB，AC上，CD与BE相交于点P，已知AD＝AE．若△ABE≌△ACD，则可添加的条件为 ．
13. 等腰三角形的两边长分别为3和4，则周长为.14. 如图，在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x轴上，且A（0，2），C（1，0），∠ACB＝90°，AC＝BC，点B在第一象限时，则点B的坐标为 ．
15. 如图，则∠A+∠B+∠C+∠D+∠E+∠F+∠G＝ ．
16. 如图，已知∠BAC＝60°，在∠BAC的平分线上截取AD＝6cm，过点D作DF⊥AB于点F，在AC上有一点E，若 ，则AE的长为 ．
17. 在Rt△ABC中，∠C＝90°，AC＝15cm，BC＝8cm，AX⊥AC于A，P、Q两点分别在边AC和射线AX上移动．当PQ＝AB，AP＝时，△ABC和△APQ全等．
18. 如图，在第一个△ABA1中，∠B＝30°，AB＝A1B，在A1B上取一点C，延长AA1到A2 ， 使得A1A2＝A1C；在A2C上取一点D，延长A1A2到A3 ， 使得A2A3＝A2D；…，按此做法依次进行下去，第2021个三角形中以A2021为顶点的内角的度数为 ．
三、解答题
-
19. △ABC在平面直角坐标系中的位置如图所示．
(1)、画出△ABC关于y轴的对称图形△DEF（点A，B，C分别与点D，E，F对应），并直接写出D，E，F三点的坐标；(2)、连接CF、CD，则△DFC的面积为 ．20. 在△ABC中，∠B＝∠A+10°，∠C＝∠B+10°，求△ABC各内角的度数.21. 如图：已知AD＝BE，BC＝EF，且BC∥EF，请说明线段AC和DF的关系．
22. 如图，在△ABC中，AB＝AC，点D，E，F分别在边AB，BC，AC上，且BE＝CF，BD＝CE．
(1)、判断△DEF的形状，并说明理由；(2)、当∠DEF＝70°时，求∠A的度数．23. 如图，在△ABC中，∠CAB的平分线AD和边BC的垂直平分线ED交于点D，过点D分别作DM⊥AB于点M，DF⊥AC，交AC的延长线于点F．
(1)、猜想CF和BM之间有何数量关系，并说明理由；(2)、求证：AB－AC＝2CF．24. 如图：
(1)、探究：如图①，在△ABC中，∠ACB＝90°，CD⊥AB于点D，若∠B＝28°，则∠ACD的度数是 ．(2)、拓展：如图②，∠MCN＝90°，射线CP在∠MCN的内部，点A、B分别存CM、CN上，分别过点A、B作AD⊥CP、BE⊥CP于点D、E，若AC＝CB，求AD、DE、BE三者间的数量关系．请说明理由；(3)、应用：如图③，点A、B分别在∠MCN的边CM、CN上，射线CP在∠MCN的内部，点D、E在射线CP上，连结AD、BE、AE，且使∠MCN＝∠ADP＝∠BEP．当AC＝BC时，△≌△；此时如果CD＝2DE，且S△CBE＝6，则△ACE的面积是 ．