黑龙江省哈尔滨市通河县2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2021-02-01 类型：期中考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 如果点P关于x轴的对称点P1的坐标为（4，5），那么点P坐标是（ ）A、（﹣5，﹣4） B、（4，﹣5） C、（﹣4，﹣5） D、（﹣4，5）3. 在等腰三角形ABC中，它的两边长分别为8cm和 3cm，则它的周长为（ ）A、19cm B、19cm 或 14cm C、11cm D、10cm4. 已知三角形的三个外角的度数比为2：3：4，则它的最大内角的度数为（ ）A、90° B、110° C、100° D、120°5. 如图，△ABC中，∠ACB＝90°，CM是高，∠MCA＝30°，若AC＝4，则AB的长度为（ ）
A、8 B、6 C、4 D、56. 如图，AB＝AC，AE＝EC，∠ACE＝28°，则∠B的度数是（ ）
A、60° B、70° C、76° D、45°7. 已知在△ABC中，点P在三角形内部，点P到三个顶点的距离相等，则点P是（ ）A、三条角平分线的交点 B、三条高线的交点 C、三条中线的交点 D、三条边垂直平分线的交点8. 下列三角形不一定全等的是（ ）A、有两个角和一条边对应相等的三角形 B、有两条边和一个角对应相等的三角形 C、斜边和一锐角对应相等的两个直角三角形 D、三条边对应相等的两个三角形9. 已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1 ， O，P2三点所构成的三角形是（ ）A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形10. 下列说法：①如果两个三角形全等，则它们必是关于某条直线成轴对称的图形；②等腰三角形的高、中线、角平分线互相重合；③若三角形一个外角的平分线平行于三角形的一边，则这个三角形为等腰三角形；④等腰三角形顶角的外角是底角的二倍；⑤等腰三角形两腰上的中线长相等．其中正确的共有（ ）A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 若一个多边形的内角和比外角和大360°，则这个多边形的边数为 ．12. 在△ABC中，AB＝4，AC＝6，D为BC边的中点，则中线AD的取值范围是 ．13. 如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为厘米．
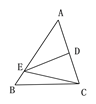14. 如图，已知等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则∠EFD＝ ．
15. 等腰三角形一腰上的高与另一腰的夹角为40°，则其顶角的度数为 ．16. 如图，在等腰直角△ABC中，∠A＝90°，AB＝AC，D为边BC中点，DE⊥DF，若四边形AEDF的面积是4，则等腰直角△ABC的面积为 ．
17.如图，AD是三角形ABC的对称轴，点E、F是AD上的两点，若BD=2，AD=3，则图中阴影部分的面积是。
18. 如果△ABC的三边长分别为7，5，3，△DEF的三边长分别为2x﹣1，3x﹣2，3，若这两个三角形全等，则x= ．19. 如图，在平面直角坐标系中，△AOB≌△COD，则点D的坐标是 ．
20. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是 ．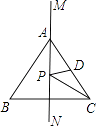
三、解答题
-
21. 如图：点 、 、 、 在一条直线上， 、 ， ，
求证： ．
22. 如图，在平面直角坐标系中，已知△ABC．
(1)、画出△ABC关于y轴的对称图形△A1B1C1；(2)、写出点A1、B1、C1的坐标；(3)、计算出△ABC的面积．23. 如图，△ABC中，AC＝BC，∠ACB＝90°，点D在AB上，点E在BC上，且AD＝BE，BD＝AC．
(1)、求证：CD＝ED(2)、直接写出图中所有是∠ACD的2倍的角．24. 如图， ， ， ，连接 ，过点 作 于 ，过点 作 于 ．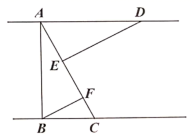
(1)、若 ，求 的度数．(2)、请直接写出线段 、 、 三者间的数量关系．25. 如图所示，∠BAC＝30°，D为角平分线上一点，DE⊥AC于E，DF∥AC，且交AB于点F．
(1)、求证：△AFD为等腰三角形；(2)、若DF＝10cm，求DE的长．
