初中数学浙教版八年级下册2.3 一元二次方程的应用 同步练习
试卷更新日期:2021-02-01 类型:同步测试
一、单选题
-
1. 某班学生毕业时,都将自己的照片向本班其他同学送一张留念,全班一共送了1260张,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1260 B、2x(x+1)=1260 C、x(x﹣1)=1260 D、x(x﹣1)=1260×22. 为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为x.那么x满足的方程为( )A、18 (1+2x)=90 B、18 (1+x) 2=90 C、18+18 (1+x)+18 (1+2x)=90 D、18+18 (1+x)+18 (1+x) 2=903. 某种花卉每盆的盈利与每盆所植的株数有一定的关系,每盆植5株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少1元,要使每盆的盈利达到14元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )A、(5+x)(4-x)=14 B、(x+5)(4+x)=14 C、(x+4)(5-x)=14 D、(x+1)(4-x)=144. 如图,在一块长为 ,宽为 的矩形 空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为 .设道路宽为 ,则以下方程正确的是( )
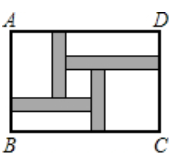 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 一个两位数,它的数值等于它的个位上的数字的平方的3倍,它的十位数字比个位数字大2.若设个位数字为x , 列出求该两位数的方程式为 .6. 有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了人.7. 某工厂七月份产值是 万元,计划九月份的产值要达到 万元,如果每月的产值的增长率相同,则增长率为 .8. 某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价____元.9. 如图,在工地边的靠墙处, 用 米长的铁栅栏围一个占地面积为 平方米的长方形临时仓库,并在其中一边上留宽为 米的大门,设无门的那边长为 米.根据题意,可建立关于x的方程是 .

三、综合题
-
10. 为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。(1)、x的值是多少?(2)、再经过几轮转发后,参与人数会超过10000人?11. 把一个足球垂直地面向上踢,t(秒)后该足球的高度h(米)适用公式h=20t-5t2(1)、经过多少秒足球重新回到地面?(2)、经过多少秒足球的高度为15米?12. 自2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日这天猪肉售价为每千克56元,比去年同一天上涨了40%.(1)、求2019年1月10日,该超市猪肉的售价为每千克多少元?(2)、现在某超市以每千克46元的价格购进猪肉,按2020年月10日价格出售,平均一天能销售100千克.为促进消费,超市决定对这批猪肉进行降价销售,经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加18千克.为了实现平均每天有950元的销售利润,超市应将每千克猪肉定为多少元?13. 某市一楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)、求平均每次下调的百分率;(2)、某人准备以开盘均价购买一套200平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.5折销售;②不打折,送2年物业管理费,物业管理费为每平方米每月5元,请问哪种方案更优惠?14. 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
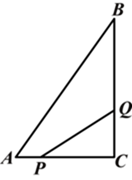 (1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?15. 阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?15. 阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
 (1)、求步道的宽.(2)、为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.已知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2 , 且区域丙为正方形,求塑胶跑道的总面积.
(1)、求步道的宽.(2)、为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.已知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2 , 且区域丙为正方形,求塑胶跑道的总面积.