初中数学浙教版七年级下册第二章二元一次方程组单元检测

试卷更新日期：2021-02-01 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列方程中，是二元一次方程的是（）

A、2x-y=3 B、x+1=2 C、 $\frac{3}{x}$ +3y=5 D、x+y+z=6

查看试题解析
2. 用加减法解方程组 ${\begin{array}{l} 2 x - y = 2 ① \\ x + y = 4 ② \end{array}$ 时，方程① $+$ ②得 $($ $)$

A、 $2 y = 2$ B、 $3 x = 6$ C、 $x - 2 y = - 2$ D、 $x + y = 6$

查看试题解析
3. 下列方程组中，属于二元一次方程组的是（）

A、 ${\begin{cases} x + y = 5 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x + y = 2 \\ y - z = 8 \end{cases}$ C、 ${\begin{cases} x y = 4 \\ y = 1 \end{cases}$ D、 ${\begin{cases} x^{2} - 1 = 0 \\ x + y = 3 \end{cases}$

查看试题解析
4. 二元一次方程2x－y＝11的一个解可以是（）

A、 ${\begin{array}{l} x = 1 \\ y = 9 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 7 \\ y = - 3 \end{array}$

查看试题解析
5. 已知 $2 x - y = 1$ ，用含 $x$ 的代数式表示 $y$ 正确的是（）

A、 $y = 2 x + 1$ B、 $x = \frac{y + 1}{2}$ C、 $y = 1 - 2 x$ D、 $y = 2 x - 1$

查看试题解析
6. 用代入法解方程组 ${\begin{cases} y = 1 - x \\ x - 2 y = 4 \end{cases}$ 时，代入正确的是（）

A、x－2－x＝4 B、x－2－2x＝4 C、x－2＋2x＝4 D、x－2＋x＝4

查看试题解析
7. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程组 ${\begin{array}{l} 3 x + 2 y = m \\ m x - y = n \end{array}$ 的解，则m﹣n的值为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 若 ${(a + 3)}^{2} + | b - 2 | = 0$ ，则 $a^{b}$ 的值为（）

A、6 B、－6 C、9 D、-9

查看试题解析
9. 如图，在长为15，宽为12的矩形中，有形状、大小完全相同的5个小矩形，则图中阴影部分的面积为（）

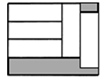A、10 B、15 C、45 D、25

查看试题解析
10. 已知一个四位数的十位数字加1等于它的个位数字，个位数字加1等于它的百位数字，把这个四位数倒序排列所成的数与原数的和等于10769，则该四位数的数字之和为（　　）。

A、25 B、24 C、33 D、34

查看试题解析

二、填空题

11. 如图所示，下列各组数的题序已经填入图中适当的位置。① ${\begin{cases} x = 1 \\ y = 0 \end{cases}$ ；② ${\begin{cases} x = - 2 \\ y = 2 \end{cases}$ ；③ ${\begin{cases} x = - \frac{1}{2} \\ y = 1 \end{cases}$ ；④ ${\begin{cases} x = \frac{1}{2} \\ y = - \frac{1}{2} \end{cases}$ ；则二元一次方程组 ${\begin{cases} x = - y \\ 2 x - 2 = - 3 y \end{cases}$ 的解是。

查看试题解析
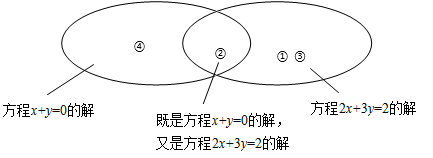12. 如图，已知天平1和天平2的两端都保持平衡．要使天平3两端也保持平衡，则天平3的右托盘上应放个圆形。

查看试题解析
13. 关于 $x, y$ 的方程 $2 x^{m + 1} + 3 y^{n - 1} = 5$ 是二元一次方程，则 $m - n =$ .

查看试题解析
14. 弟弟对哥哥说：“我像你这么大的时候你已经20岁.”哥哥对弟弟说：“我像你这么大的时候你才5岁.”求弟弟和哥哥的年龄.设这一年弟弟x岁，哥哥y岁，根据题意可列出二元一次方程组是.

查看试题解析
15. 从甲地到乙地有一段上坡和一段平路，如果保持上坡每分钟走50米，平路每分钟走60米，下坡每分钟走80米，那么从甲地到乙地需36分，从乙地到甲地需30分，则甲地到乙地的全程是米.

查看试题解析
16. 一根金属棒在0℃时的长度是b（m），温度每升高1℃，它就伸长a（m），当温度为x（℃）时，金属棒的长度y可用公式y=ax+b计算.已测得当x=100℃时，y=2.002m；当x=500℃时，y=2.01m.若这根金属棒加热后长度伸长到2.015m，则此时金属棒的温度是℃.

查看试题解析

三、综合题

17. 解下列二元一次方程组：

(1)、

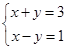(2)、 ${\begin{matrix} \frac{m + n}{3} - \frac{m - n}{4} = 3 ， \\ \frac{m + n}{2} - \frac{m - n}{3} = 5 \end{matrix}$

查看试题解析
18. 课本里，用代入法解二元一次方程组 ${\begin{matrix} x - y = 2 \\ 2 x + y = 7 \end{matrix}$ 的过程是用下面的框图表示：
根据以上思路，请用代入法求出方程组 ${\begin{matrix} x - y = 0 \\ | x - 2 y | = 2 \end{matrix}$ 的解（不用画框架图）.

查看试题解析
19. 我国明代数学家程大位的名著《算法统宗》里有一道著名算题，原文如下：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”．译文为：“有100个和尚分100个馒头，正好分完，如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各几人？”试用列方程（组）解应用题的方法求出问题的解．

查看试题解析

20. 杭州市实行“五水共治”，为鼓励市民节约用水，居民生活用水按阶梯式水价计费．下表是居民“一户一表”生活用水阶梯式计费价格表部分信息：

每户每月用水量	自来水销售价格 (单位：元/吨)	污水处理价格 (单位：元/吨)
17吨及以下	a	0.80
超过17吨但不超过30吨的部分	b	0.80
超过30吨的部分	6.00	0.80

(说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费)

已知小王家2019年四月份用水20吨，交水费66元；五月份用水25吨，交水费91元。

(1)、求a，b的值。

(2)、随着夏天的到来，用水量将增加，小王家六月份的水费是家庭月收入的2%，若小王家的月收入为9200元，求小王家六月份的用水量是多少吨？

查看试题解析

21. 今有鸡兔同笼，上有二十六头，下有八十二足，问鸡兔各几何？

(1)、根据上面文字求出鸡兔各有多少只？

(2)、若设A为鸡兔总共只数，B为鸡兔总共足数，请你运用方程组探索兔数、A、B之间的关系，并将你发现的结论用等式表示出来？

查看试题解析

22. 为了预防新型冠状病毒感染，市场上防护口罩出现热销.某药店购进了一批A，B两种不同型号口罩进行销售.下表是甲、乙两人购买A，B两种型号口罩的情况:

	A型号数量（单位：个）	B型号数量（单位：个）	总售价（单位：元）
甲	1	3	26
乙	3	2	29

(1)、求一个A型口罩和一个B型口罩的售价各是多少元?

(2)、小王准备购买A型口罩35个，B型口罩15个；小丽准备购买A型口罩37个，B型口罩13个，求他们各需付款多少元?

查看试题解析

23. 某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)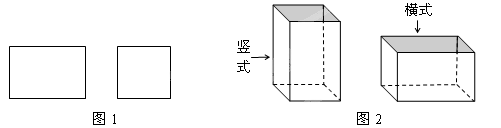

(1)、如果加工竖式铁容器与横式铁容器各1个，则共需要长方形铁片张，正方形铁片张.

(2)、现有长方形铁片2014张，正方形铁片1176张，如果加工成这两种铁容器，刚好铁片全部用完，那么加工的竖式铁容器、横式铁容器各有多少个?

(3)、把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与如图相同的长方形铁片和正方形铁片，已知每张铁板可做成3个长方形铁片或4个正方形铁片，也可以将一张铁板做成1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒，最多可以加工成多少个铁盒?

查看试题解析
24.

(1)、若方程组 ${\begin{array}{l} 2 a - 3 b = 4.7 \\ 3 a + 5 b = 19.4 \end{array}$ 的解是 ${\begin{array}{l} a = 4.3 \\ b = 1.3 \end{array}$ ，则不解方程组写出方程组 ${\begin{array}{l} 2 (x - 1) - 3 (y + 1) = 4.7 \\ 3 (x - 1) + 5 (y + 1) = 19.4 \end{array}$ 的解为.

(2)、若关于 $x, y$ 的方程组 ${\begin{array}{l} 5 x + 3 a y = 16 \\ - b x + 4 y = 15 \end{array}$ ，（其中 $a, b$ 是常数）的解为 ${\begin{array}{l} x = 6 \\ y = 7 \end{array}$ ，解方程组 ${\begin{array}{l} 5 (x + 1) + 3 a (x - 2 y) = 16 \\ - b (x + 1) + 4 (x - 2 y) = 15 \end{array}$ .

(3)、若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 4 \\ y = 6 \end{array}$ ，则方程组 ${\begin{array}{l} 4 a_{1} x + 3 b_{1} y = 5 c_{1} \\ 4 a_{2} x + 3 b_{2} y = 5 c_{2} \end{array}$ 的解为.

查看试题解析

初中数学浙教版七年级下册 第二章二元一次方程组 单元检测

一、单选题

二、填空题

三、综合题

初中数学浙教版七年级下册第二章二元一次方程组单元检测