甘肃省天水市甘谷县2020-2021学年高三上学期理数第四次检测试卷
试卷更新日期:2021-01-31 类型:月考试卷
一、单选题
-
1. 已知复数z满足z(1+2i)=i,则复数 在复平面内对应点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知集合 , ,则 的子集个数为( )A、2 B、3 C、4 D、83. “ ”是“对任意的正数 , ”的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 若正数m,n满足2m+n=1,则 + 的最小值为( )A、3+2 B、3+ C、2+2 D、35. 若实数x,y满足约束条件 ,则z=3x+2y的最大值是( )A、-1 B、1 C、10 D、126. 函数 的图象大致为( )A、 B、
B、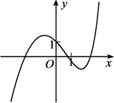 C、
C、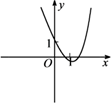 D、
D、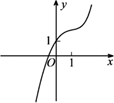 7. 中国传统扇文化有着极其深厚的底蕴. 一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形的面积为 ,圆面中剩余部分的面积为 ,当 与 的比值为 时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为( )
7. 中国传统扇文化有着极其深厚的底蕴. 一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形的面积为 ,圆面中剩余部分的面积为 ,当 与 的比值为 时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为( ) A、 B、 C、 D、8. 若函数f(x)= Asin( x +φ)(A >0, > 0,0<φ <π)的部分图像如图所示,则函数f(x)图像的一条对称轴是( )
A、 B、 C、 D、8. 若函数f(x)= Asin( x +φ)(A >0, > 0,0<φ <π)的部分图像如图所示,则函数f(x)图像的一条对称轴是( ) A、x= B、x=- C、x= D、9. 设向量 , ,则下列结论中正确的是( )A、 B、 C、 与 的夹角为 D、 在 方向上的投影为10. 已知正项数列 满足: , ,则使 成立的 的最大值为( )A、3 B、4 C、24 D、2511. 已知函数 在定义域上的值不全为零,若函数 的图象关于 对称,函数 的图象关于直线 对称,则下列式子中错误的是( )A、 B、 C、 D、12. 若函数 ,则满足 恒成立的实数 的取值范围为( )A、 B、 C、 D、
A、x= B、x=- C、x= D、9. 设向量 , ,则下列结论中正确的是( )A、 B、 C、 与 的夹角为 D、 在 方向上的投影为10. 已知正项数列 满足: , ,则使 成立的 的最大值为( )A、3 B、4 C、24 D、2511. 已知函数 在定义域上的值不全为零,若函数 的图象关于 对称,函数 的图象关于直线 对称,则下列式子中错误的是( )A、 B、 C、 D、12. 若函数 ,则满足 恒成立的实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 设 是等差数列,且a1=3, a2+a5= 36,则 的通项公式为14. 的内角 的对边分别为 .若 ,则 的面积为.15. 在边长为2的正方形 中, 为 的中点, 交 于 .若 ,则 .

16. 在 中,角 、 、 所对的边分别为 、 、 ,若 , ,则当角 取最大值时, 的周长为.三、解答题
-
17. 在△ABC中,a=3,b−c=2,cosB= .
(Ⅰ)求b,c的值;
(Ⅱ)求sin(B–C)的值.
18. 记 为等差数列 的前 项和,已知 , .(1)、求 的通项公式;(2)、求 ,并求 的最小值.19. 已知数列 的前 项和 ,满足(1)、求数列 的通项公式;(2)、求数列 的前 项和20. 在① ,② ,③ 三个条件中任选一个,补充在下面的问题中,并解决该问题.在 中,内角 的对边分别是 ,且满足 ,
(1)、若 ,求 的面积;(2)、求 的取值范围.