人教版数学九年级下册 第二十八章 锐角三角函数 单元测试
试卷更新日期:2021-01-31 类型:单元试卷
一、单选题
-
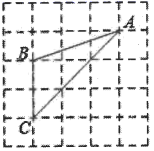
1. 若sin(75°-θ)的值是 ,则θ=( )A、15° B、30° C、45° D、60°2. 如果a是锐角,且cosa= ,那么sina的值是( )A、 B、 C、 D、3. 的值等于( )A、 B、 C、 D、4. 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
 A、 B、 C、2 D、5. 如图,△ABC内接于⊙O,I是△ABC的内心,AI的延长线交⊙O于点D,连接DB、DC,若AB是⊙O的直径,OI⊥AD,则 的值为( )
A、 B、 C、2 D、5. 如图,△ABC内接于⊙O,I是△ABC的内心,AI的延长线交⊙O于点D,连接DB、DC,若AB是⊙O的直径,OI⊥AD,则 的值为( )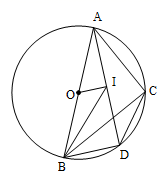 A、 B、 C、 D、6. 如图,在 中, , , ,若 是 边上的动点,则 的最小值( )
A、 B、 C、 D、6. 如图,在 中, , , ,若 是 边上的动点,则 的最小值( )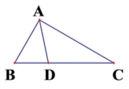 A、 B、6 C、 D、47. 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( )
A、 B、6 C、 D、47. 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( )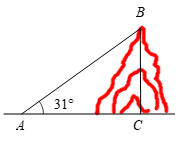 A、 B、 C、 D、8. 如图,在平面直角坐标系中,将边长为1的正六边形 绕点O顺时针旋转i个45°,得到正六边形 ,则正六边形 的顶点 的坐标是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,将边长为1的正六边形 绕点O顺时针旋转i个45°,得到正六边形 ,则正六边形 的顶点 的坐标是( )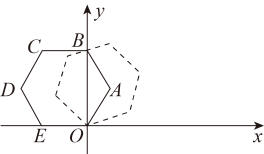 A、 B、 C、 D、9. 如图,等边三角形ABC和正方形ADEF都内接于 ,则 ( )
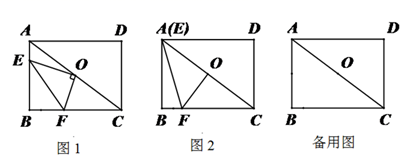
A、 B、 C、 D、9. 如图,等边三角形ABC和正方形ADEF都内接于 ,则 ( ) A、 B、 C、 D、10. 如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC= ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
A、 B、 C、 D、10. 如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC= ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )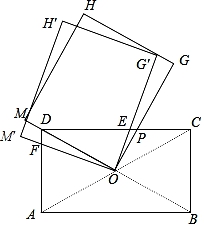 A、y= x B、y= x C、y= x D、y= x
A、y= x B、y= x C、y= x D、y= x二、填空题
-
11. 计算: .12. 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=.
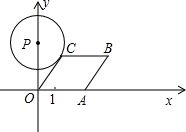 13. 已知sina= (a为锐角),则tana=14. 某斜坡的坡度 ,则它的坡角是度.15. 如图,在 中,AB=AC=10, ,点D为BC边上的动点(点D不与点B,C重合),以D为顶点作 ,射线DE交AC边于点E,若BD=4,则AE= .
13. 已知sina= (a为锐角),则tana=14. 某斜坡的坡度 ,则它的坡角是度.15. 如图,在 中,AB=AC=10, ,点D为BC边上的动点(点D不与点B,C重合),以D为顶点作 ,射线DE交AC边于点E,若BD=4,则AE= .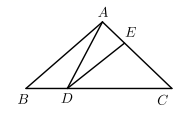 16. 如图,在 中, , , .将 以点 为中心,逆时针旋转60°,得到 ,连接 .则 .
16. 如图,在 中, , , .将 以点 为中心,逆时针旋转60°,得到 ,连接 .则 .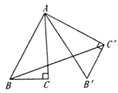 17. 如图,在 的网格中,每一个小正方形的边长都是1,点 、 、 、 都在格点上,连接 , 相交于 ,那么 的大小是.
17. 如图,在 的网格中,每一个小正方形的边长都是1,点 、 、 、 都在格点上,连接 , 相交于 ,那么 的大小是.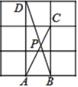
三、计算题
-
18. 计算 .
四、解答题
-
19. 如图,在 中, , , ,求 的面积.
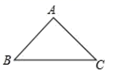 20. 如图,在 处的正东方向有--港口 .某巡逻艇从 处沿着北偏东 方向巡逻,到达 处时接到命令,立刻在 处沿东南方向以 海里/时的速度行驶 小时到达港口B.求 间的距离.
20. 如图,在 处的正东方向有--港口 .某巡逻艇从 处沿着北偏东 方向巡逻,到达 处时接到命令,立刻在 处沿东南方向以 海里/时的速度行驶 小时到达港口B.求 间的距离.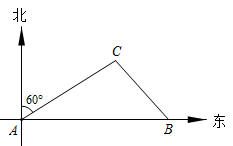 21. 图①是一辆吊车的实物图,图②是其工作示意图, 是可以伸缩的起重臂,其转动点A离地面 的高度 为 .当起重臂 长度为 ,张角 为118°时,求操作平台C离地面的高度.(结果保留小数点后一位)(参考数据: , , )
21. 图①是一辆吊车的实物图,图②是其工作示意图, 是可以伸缩的起重臂,其转动点A离地面 的高度 为 .当起重臂 长度为 ,张角 为118°时,求操作平台C离地面的高度.(结果保留小数点后一位)(参考数据: , , )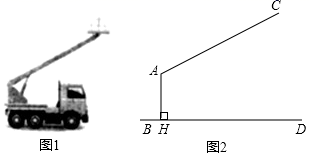 22. 如图,一根电线杆PQ直立在山坡上,从地面的点A看,测得杆顶端点P的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和30°,求电线杆PQ的高度.(结果保留根号).
22. 如图,一根电线杆PQ直立在山坡上,从地面的点A看,测得杆顶端点P的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和30°,求电线杆PQ的高度.(结果保留根号).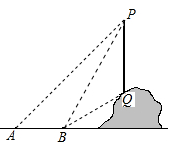
五、综合题
-