2016年四川省南充市高考数学一模试卷

试卷更新日期：2016-07-13 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合A={x|1＜x＜4}，集合B={x|（x﹣3）（x+1）＜0}，则A∩B=（　　）

A、{x|﹣1＜x＜4} B、{x|﹣1＜x＜1} C、{x|1＜x＜3} D、{x|﹣1＜x＜3}

查看试题解析
2. 设i是虚数单位，则复数 $\frac{{(1 + i)}^{2}}{1 - i}$ =（　　）

A、1+i B、1﹣i C、﹣1﹣i D、﹣1+i

查看试题解析
3. 已知命题P：∀x∈R，e^x﹣x﹣1＞0，则￢P是（　　）

A、∀x∈R，e^x﹣x﹣1＜0 B、∃x₀∈R，e $x_{0}$ ﹣x₀﹣1≤0 C、∃x₀∈R，e $x_{0}$ ﹣x₀﹣1＜0 D、∀x∈R，e^x﹣x﹣1≤0

查看试题解析
4. 下列函数中，满足“f（xy）=f（x）+f（y）”的单调递减函数是（　　）

A、f（x）=lnx B、f（x）=﹣x³ C、f（x）= $\log_{\frac{1}{2}}$ x D、f（x）=3^﹣x

查看试题解析
5.
如图的程序图的算法思路中是一种古老而有效的算法﹣﹣辗转相除法，执行改程序框图，若输入的m，n的值分别为30，42，则输出的m=（　　）

A、0 B、2 C、3 D、6

查看试题解析
6. 为了得到函数y= $\frac{1}{2}$ sin4x﹣ $\frac{\sqrt{3}}{2}$ cos4x的图象，可以将函数y=sin4x的图象（　　）

A、向右平移 $\frac{π}{12}$ 个单位 B、向左平移 $\frac{π}{12}$ 个单位 C、向右平移 $\frac{π}{3}$ 个单位 D、向左平移 $\frac{π}{3}$ 个单位

查看试题解析
7.
某几何体的三视图如图所示，则此几何体的体积等于（　　）

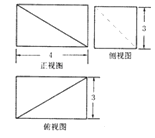A、45 B、36 C、30 D、6

查看试题解析
8. 春节前，某市一过江大桥上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的6秒内任一时刻等可能发生，然后每串彩灯以6秒内间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过3秒的概率是（　　）

A、 $\frac{7}{8}$ B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
9. 已知F是抛物线y²=4x的焦点，点A，B在该抛物线上且位于x轴的两侧，OA⊥OB（其中O为坐标原点），则△AOB与△AOF面积之和的最小值是（　　）

A、16 B、8 $\sqrt{3}$ C、8 $\sqrt{5}$ D、18

查看试题解析
10. 函数f′（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＜0时，xf′（x）+f（x）＞0，则使得f（x）＜0成立的x的取值范围是（　　）

A、（﹣∞，﹣1）∪（0，1） B、（﹣1，0）∪（1，+∞） C、（﹣∞，﹣1）∪（1，+∞） D、（﹣1，0）∪（0，1）

查看试题解析

二、填空题

11. 在（3﹣x）⁵的展开式中，含x³的项的系数是用数字作答）

查看试题解析
12. 已知α∈（0， $\frac{π}{2}$ ），β∈（0， $\frac{π}{2}$ ），且cosα= $\frac{1}{7}$ ， cos（α+β）=﹣ $\frac{11}{14}$ ，则sinβ=

查看试题解析
13. 已知实数x，y满足 $\{\begin{matrix} 2 x + y - 2 \geq 0 \\ x - 2 y + 4 \geq 0 \\ 3 x - y - 3 \leq 0 \end{matrix}$ ，则x²+y²的最大值为．

查看试题解析
14. 设四边形ABCD为平行四边形，| $\vec{A B}$ |=8，| $\vec{A D}$ |=3，若点M，N满足 $\vec{D M}$ =3 $\vec{M C}$ ， $\vec{B N}$ =2 $\vec{N C}$ ，则 $\vec{A M}$ • $\vec{M N}$ =

查看试题解析
15. 设S为复数集C的非空子集．如果
（1）S含有一个不等于0的数；
（2）∀a，b∈S，a+b，a﹣b，ab∈S；
（3）∀a，b∈S，且b≠0， $\frac{a}{b}$ ∈S，那么就称S是一个数域．
现有如下命题：
①如果S是一个数域，则0，1∈S；
②如果S是一个数域，那么S含有无限多个数；
③复数集是数域；
④S={a+b $\sqrt{2}$ |a，b∈Q，}是数域；
⑤S={a+bi|a，b∈Z}是数域．
其中是真命题的有（写出所有真命题的序号）．

查看试题解析

三、解答题

16. 已知数列{a_n}满足a₁=1，a_n+1=2a_n+1．
（1）求数列{a_n}的通项公式；
（2）令b_n= $\frac{1}{2}$ n（a_n+1），求数列{b_n}的前n项和T_n ．

查看试题解析
17. 某高校文学院和理学院的学生组队参加大学生电视辩论赛，文学院推荐了2名男生，3名女生，理学院推荐了4名男生，3名女生，文学院和理学院所推荐的学生一起参加集训，由于集训后学生水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队．
（1）求文学院至少有一名学生入选代表队的概率；
（2）某场比赛前，从代表队的6名学生在随机抽取4名参赛，记X表示参赛的男生人数，求X的分布列与数学期望．

查看试题解析
18. 已知函数f（x）=sinx（sinx+ $\sqrt{3}$ cosx）．
（1）求f（x）的最小正周期和最大值；
（2）在锐角三角形ABC中，角A，B，C的对边分别为a，b，c，若f（ $\frac{A}{2}$ ）=1，a=2 $\sqrt{3}$ ，求三角形ABC面积的最大值．

查看试题解析
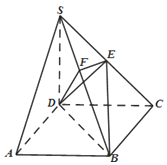
19.
如图，在四棱锥S﹣ABCD中，底面ABCD是矩形，SD=DC=2AD，侧棱SD⊥底面ABCD，点E是SC的中点，点F在SB上，且EF⊥SB．
（1）求证：SA∥平面BDE；
（2）求证SB⊥平面DEF；

查看试题解析
20. 已知圆F₁：（x+1）²+y²=1，圆F₂：（x﹣1）²+y²=25，动圆P与圆F₁外切并且与圆F₂内切，动圆圆心P的轨迹为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）若曲线C与x轴的交点为A₁ ， A₂ ，点M是曲线C上异于点A₁ ， A₂的点，直线A₁M与A₂M的斜率分别为k₁ ， k₂ ，求k₁k₂的值．

查看试题解析
21. 设函数f（x）= $\frac{e^{x}}{x^{2}}$ +k（ $\frac{2}{x}$ +lnx）（k为常数）．
（1）当k=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当k≥0时，求函数f（x）的单调区间；
（3）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围．

查看试题解析