天津市和平区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-10-19 类型:期末考试
一、选择题
-
1. 如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
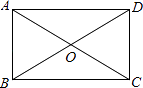 A、∠ABC=90° B、AC=BD C、OA=OB D、OA=AB2. 若 在实数范围内有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x≠1 D、x>﹣13. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:
A、∠ABC=90° B、AC=BD C、OA=OB D、OA=AB2. 若 在实数范围内有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x≠1 D、x>﹣13. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:甲
乙
丙
丁
平均数 (cm)
561
560
561
560
方差s2(cm2)
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁4. 某个一次函数的图象与直线y= x平行,并且经过点(﹣2,﹣4),则这个一次函数的解析式为( )A、y=﹣ x﹣5 B、y= x+3 C、y= x﹣3 D、y=﹣2x﹣85. 直线y=2x+6与x轴的交点坐标为( )
A、(﹣3,0) B、(3,0) C、(0,6) D、(0,﹣3)6. 下列计算错误的是( )A、 ÷ =2 B、( + )× =2 +3 C、(4 ﹣3 )÷2 =2﹣ D、( +7)( ﹣7)=﹣27. 为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )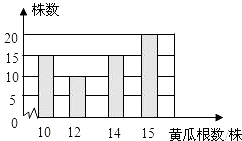 A、12 B、12.5 C、13 D、148. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列判断:
A、12 B、12.5 C、13 D、148. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列判断:①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
A、0个 B、1个 C、2个 D、3个10. 在菱形ABCD中,E、F分别在BC和CD上,且△AEF是等边三角形,AE=AB,则∠BAD等于( )A、95° B、100° C、105° D、120°11. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )A、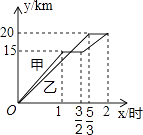 B、
B、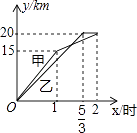 C、
C、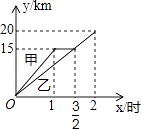 D、
D、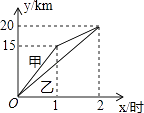 12. 给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:
12. 给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:①如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是平行四边形.
②如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是菱形
③在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,则中点四边形EFGH是正方形
其中,正确的有( )
 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
13. 直角三角形斜边上的中线等于斜边的 .14. 计算: ÷ = .15. 已知正比例函数y=kx(k是常数,k≠0),y随x的增大而减小,写出一个符合条件的k的值为 .
16. 某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项素质测试,两人的两项测试成绩如表所示.测试项目
测试成绩
A
B
面试
90
95
综合知识测试
85
80
根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么(填A或B)将被录用.
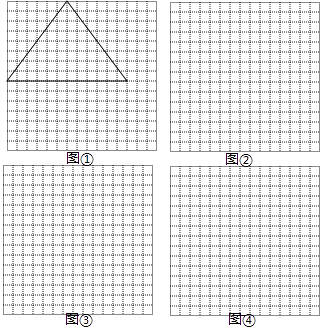
17. 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为 .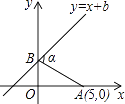 18. 如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.
18. 如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.在图②③④中分别画出一个以格点为顶点,边长都为整数的锐角三角形,并在每条边上标出其长度(图①﹣④中的三角形互不全等)
三、解答题
-
19. 计算:
(1)、 ﹣(2)、 × ÷ .20. 在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数
0
1
2
3
4
人数
3
13
16
17
1
(1)、求这50个样本数据的平均数、众数和中位数:(2)、根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.21. 如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.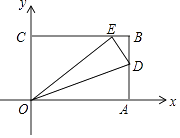 (1)、OA的长= , OE的长= , CE的长= , AD的长=;(2)、设点P在x轴上,且OP=EP,求点P的坐标.22. 如图,在四边形ABCD中,∠B=∠C,点E,F分别在边AB,BC上,AE=DF=DC.
(1)、OA的长= , OE的长= , CE的长= , AD的长=;(2)、设点P在x轴上,且OP=EP,求点P的坐标.22. 如图,在四边形ABCD中,∠B=∠C,点E,F分别在边AB,BC上,AE=DF=DC. (1)、若∠DFC=70°,则∠C的大小=(度),∠B的大小=(度);(2)、求证:四边形AEFD是平行四边形;(3)、若∠FDC=2∠EFB,则四边形AEFD一定是“菱形、矩形、正方形”中的 .23. 一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.
(1)、若∠DFC=70°,则∠C的大小=(度),∠B的大小=(度);(2)、求证:四边形AEFD是平行四边形;(3)、若∠FDC=2∠EFB,则四边形AEFD一定是“菱形、矩形、正方形”中的 .23. 一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.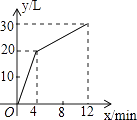 (1)、当0≤x≤4时,y关于x的函数解析式为;(2)、当4<x≤12时,求y关于x的函数解析式;(3)、每分钟进水升,每分钟出水升,从某时刻开始的9分钟时容器内的水量是升.24. 已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.
(1)、当0≤x≤4时,y关于x的函数解析式为;(2)、当4<x≤12时,求y关于x的函数解析式;(3)、每分钟进水升,每分钟出水升,从某时刻开始的9分钟时容器内的水量是升.24. 已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.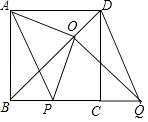 (1)、如图,点P在线段BC上,
(1)、如图,点P在线段BC上,①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)、若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.25. 如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.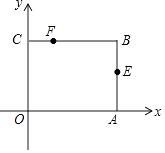 (1)、点E的坐标为 , 点F的坐标为;(2)、点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
(1)、点E的坐标为 , 点F的坐标为;(2)、点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,①点E′的坐标为 , 点F′的坐标为;
②求直线E′F′的解析式;
(3)、若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.