湖北省襄阳市宜城市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-10-19 类型:期末考试
一、选择题
-
1. 下列二次根式能与 合并的是( )A、 B、 C、 D、2. 下列计算错误的是( )A、 + = B、 × =2 C、 ÷ = D、 =23. 放学以后,小明和小强从学校分手,分别沿东南方向和西南方向回家,若小明和小强行走的速度都是40米/分,小明用15分钟到家,小强用20分钟到家,小明家和小强家的距离为( )
A、600米 B、800米 C、1000米 D、不能确定4. 下表是某校合唱团成员的年龄分布:年龄(岁)
13
14
15
16
频数
5
15
x
10﹣x
则合唱团成员年龄的中位数和众数分别是( )
A、14,15 B、14,14 C、15,14 D、15,155. 为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的方差是( )A、 B、10 C、 D、6. 点P(x,y)在第一象限内,且x+y=6,点A的坐标为(4,0).设△OPA的面积为S,则下列图象中,能正确反映面积S与x之间的函数关系式的图象是( )A、 B、
B、 C、
C、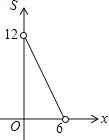 D、
D、 7. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
7. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( ) A、8 B、10 C、12 D、148. 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A、8 B、10 C、12 D、148. 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( ) A、4.8 B、5 C、6 D、7.29. 已知一次函数y=ax+5和y=bx+3,假设a>0且b<0,则这两个一次函数的图象的交点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A、4.8 B、5 C、6 D、7.29. 已知一次函数y=ax+5和y=bx+3,假设a>0且b<0,则这两个一次函数的图象的交点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )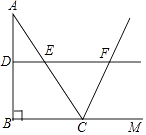 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 若点M(k﹣1,k+1)在第三象限内,则一次函数y=(k﹣1)x+k的图象不经过第象限.13. 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件使其成为菱形(只填一个即可).
 14. 某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是 .15. 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD= BC,连接DM,DN,MN,若AB=6,则DN= .
14. 某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是 .15. 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD= BC,连接DM,DN,MN,若AB=6,则DN= .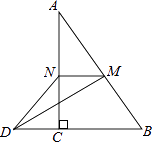 16. 在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等于 .
16. 在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等于 .三、解答题
-
17. 已知x=2+ ,求代数式(7﹣4 )x2+(2﹣ )x﹣ 的值.
18. 某快餐店共有10名员工,所有员工工资的情况如下表:人员
店长
厨师甲
厨师乙
会计
服务员甲
服务员乙
勤杂工
人数
1
1
1
1
1
3
2
工资额
20000
7000
4000
2500
2200
1800
1200
请解答下列问题:
(1)、餐厅所有员工的平均工资是;所有员工工资的中位数是 .(2)、用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?(3)、去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?19. 如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.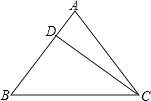 20. 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.
20. 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示. (1)、甲的速度是km/h;(2)、当1≤x≤5时,求y乙关于x的函数解析式;(3)、当乙与A地相距240km时,甲与A地相距km.21. 如图,在▱ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)、甲的速度是km/h;(2)、当1≤x≤5时,求y乙关于x的函数解析式;(3)、当乙与A地相距240km时,甲与A地相距km.21. 如图,在▱ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点. (1)、求证:△ABE≌△CDF;(2)、当四边形AECF为菱形时,求出该菱形的面积.22. 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)、求证:△ABE≌△CDF;(2)、当四边形AECF为菱形时,求出该菱形的面积.22. 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P. (1)、求证:AP=BQ;(2)、在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.23. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
(1)、求证:AP=BQ;(2)、在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.23. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:车型 目的地 A村(元/辆) B村(元/辆) 大货车 800 900 小货车 400 600
(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)、在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.24. 如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G. (1)、求证:△DOK≌△BOG;(2)、探究线段AB、AK、BG三者之间的关系,并证明你的结论;(3)、若KD=KG,BC=2 ﹣1,求KD的长度.25. 如图,平面直角坐标系中,直线l:y=﹣ x+ 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
(1)、求证:△DOK≌△BOG;(2)、探究线段AB、AK、BG三者之间的关系,并证明你的结论;(3)、若KD=KG,BC=2 ﹣1,求KD的长度.25. 如图,平面直角坐标系中,直线l:y=﹣ x+ 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°. (1)、求A,C两点的坐标.(2)、若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(1)、求A,C两点的坐标.(2)、若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.