广西桂林市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期：2017-10-19 类型：期末考试
一、选择题
-
1. 下列各点中，位于直角坐标系第二象限的点是（ ）A、（2，1） B、（﹣2，﹣1） C、（2，﹣1） D、（﹣2，1）2. 在①平行四边形，②矩形，③菱形，④正方形中，既是轴对称图形，又是中心对称图形的是（ ）A、①②③④ B、②③ C、②③④ D、①③④3. 如图，在Rt△ABC中，∠C=90°，如果AB=5，BC=3，那么AC等于（ ）
A、 B、3 C、4 D、54. 下列条件中，能判定两个直角三角形全等的是（ ）A、一锐角对应相等 B、两锐角对应相等 C、一条边对应相等 D、两条直角边对应相等5. 如图，如果CD是Rt△ABC的中线，∠ACB=90°，∠A=50°，那么∠CDB等于（ ）
A、100° B、110° C、120° D、130°6. 如图，在▱ABCD中，对角线AC、BD相交于点O，点E是AD的中点，如果OE=2，AD=6，那么▱ABCD的周长是（ ）
A、20 B、12 C、24 D、87. 若一个多边形的内角和等于900°，则这个多边形的边数是（ ）A、8 B、7 C、6 D、58. 如图，在四边形ABCD中，对角线AC与BD交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（ ）
A、AB∥DC，AD=BC B、AD∥BC，AB∥DC C、AB=DC，AD=BC D、OA=OC，OB=OD9. 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在0.15和0.45，则口袋中白色球的个数可能是（ ）A、28 B、24 C、16 D、610. 对于函数y=x﹣1，下列结论不正确的是（ ）A、图象经过点（﹣1，﹣2） B、图象不经过第一象限 C、图象与y轴交点坐标是（0，﹣1） D、y的值随x值的增大而增大11. 函数y=2x和y=ax+4的图象相交于点A（m，3），则关于x的不等式2x＜ax+4的解集为（ ）A、x＜ B、x＜ C、x＞﹣ D、x＜﹣12. 如图，在矩形ABCD中，AB=2，AD=3，BE=1，动点P从点A出发，沿路径A→D→C→E运动，则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是（ ）
A、
B、
C、
D、
二、填空题
-
13. 如图，四边形ABCD是菱形，如果AB=5，那么菱形ABCD的周长是 ．
14. 点P（2，3）关于x轴的对称点的坐标为 ．15. 将直线y=2x向上平移4个单位，得到直线 ．16. 在一次函数y=﹣x+2的图象上有A（x1 ， y1），B（x2 ， y2）两点，若x1＞x2 ， 那么y1y2 ．17. 如图所示，已知△ABC的周长是18，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=4，则△ABC的面积是 ．
18. 如图，在边长为4的正方形ABCD中，点E是边CD的中点，AE的垂直平分线交边BC于点G，交边AE于点F，连接DF，EG，以下结论：①DF= ，②DF∥EG，③△EFG≌△ECG，④BG= ，正确的有：（填写序号）
三、解答题
-
19. 如图，在▱ABCD中，AE=CF．
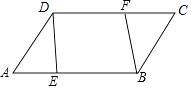(1)、求证：△ADE≌△CBF；(2)、求证：四边形BFDE为平行四边形．20. 如图，四边形草坪ABCD中，∠B=90°，AB=24m，BC=7m，CD=15m，AD=20m．
(1)、判断∠D是否是直角，并说明理由．(2)、求四边形草坪ABCD的面积．21. 某校为了解八年级学生的视力情况，对八年级的学生进行了一次视力调查，并将调查数据进行统计整理，绘制出如下频数分布表和频数分布直方图的一部分．视力
频数（人）
频率
4.0≤x＜4.3
20
0.1
4.3≤x＜4.6
40
0.2
4.6≤x＜4.9
70
0.35
4.9≤x＜5.2
a
0.3
5.2≤x＜5.5
10
b
(1)、在频数分布表中，a= ， b=；(2)、将频数分布直方图补充完整；(3)、若视力在4.6以上（含4.6）均属正常，求视力正常的人数占被调查人数的百分比是多少？
22. 我国是一个严重缺水的国家．为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过6吨时，水价为每吨2元，超过6吨时，超过的部分按每吨3元收费．该市某户居民5月份用水x吨，应交水费y元．(1)、若0＜x≤6，请写出y与x的函数关系式．(2)、若x＞6，请写出y与x的函数关系式．(3)、如果该户居民这个月交水费27元，那么这个月该户用了多少吨水？23. △ABC在平面直角坐标系中的位置如图所示，△ABC的顶点均在格点上，其中每个小正方形的边长为1个单位长度，将△ABC绕原点O旋转180°得△A1B1C1 ．
(1)、在图中画出△A1B1C1；(2)、写出点A1的坐标；(3)、求出点C所经过的路径长．24. 如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．
(1)、求证：四边形AECF是菱形；(2)、若AB= ，∠DCF=30°，求四边形AECF的面积．（结果保留根号）25. 甲，乙两辆汽车分别从A，B两地同时出发，沿同一条公路相向而行，已知甲车匀速行驶；乙车出发2h后休息，与甲车相遇后继续行驶，结果同时分别到达B，A两地．设甲、乙两车与B地的距离分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲 ， y乙与x之间的函数图象如图所示，结合图象解答下列问题：
(1)、当0＜x＜2时，求乙车的速度；(2)、求乙车与甲车相遇后y乙与x的关系式；(3)、当两车相距20km时，直接写出x的值．26. 如图，在平面直角坐标系xOy中，已知直线AB：y= x+4交x轴于点A，交y轴于点B．直线CD：y=﹣ x﹣1与直线AB相交于点M，交x轴于点C，交y轴于点D．
(1)、直接写出点B和点D的坐标；(2)、若点P是射线MD上的一个动点，设点P的横坐标是x，△PBM的面积是S，求S与x之间的函数关系；(3)、当S=20时，平面直角坐标系内是否存在点E，使以点B、E、P、M为顶点的四边形是平行四边形？若存在，请直接写出所有符合条件的点E的坐标；若不存在，说明理由．