福建省莆田市秀屿区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-10-19 类型：期末考试

进入 出卷网 下载

一、精心选一选

  • 1. 下列二次根式中，最简二次根式是（   ）
    A、8 B、19 C、a2 D、a2+1

    查看试题解析

  • 2. 已知平行四边形ABCD的周长为32，AB=4，则BC的长为（   ）
    A、4 B、12 C、24 D、28

    查看试题解析

  • 3. 下列数据中，不能作为直角三角形三边长的是（   ）
    A、7、24、25 B、6、8、10 C、9、12、15 D、5、12、15

    查看试题解析

  • 4. 一位经销商计划进一批“运动鞋”，他到眉山的一所学校里对初二的100名男生的鞋号进行了调查，经销商最感兴趣的是这组鞋号的（   ）
    A、中位数 B、平均数 C、方差 D、众数

    查看试题解析

  • 5. 下列函数中，y随x增大而减少的是（   ）
    A、y=2x﹣1 B、y=﹣x+3 C、y= 12 x+2 D、y=2x

    查看试题解析

  • 6. 下列说法错误的是（   ）
    A、顺次连接矩形各边的中点所成的四边形是菱形 B、四个角都相等的四边形是矩形 C、对角线互相垂直且相等的四边形是正方形 D、一组对边平行且相等的四边形是平行四边形

    查看试题解析

  • 7. 如图，▱ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为（   ）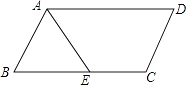

    A、1 B、2 C、3 D、4

    查看试题解析

  • 8. 一个寻宝游戏的寻宝通道由正方形ABCD的边组成，如图1所示．为记录寻宝者的行进路线，在AB的中点M处放置了一台定位仪器，设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（   ）

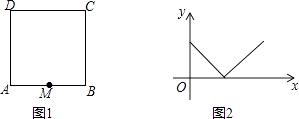    A、A→B B、B→C C、C→D D、D→A

    查看试题解析

二、细心填一填

  • 9. 二次根式 2x+4 有意义，则x的取值范围是 ．

    查看试题解析

  • 10. 一次函数y=﹣2x+3的图象不经过第象限．

    查看试题解析

  • 11. 如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：


    甲

    乙

    丙

    丁

    平均数 x¯ （cm）

    375

    350

    375

    350

    方差s2

    12.5

    13.5

    2.4

    5.4

    根据表中数据，要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛，应该选择 ．

    查看试题解析

  • 12. 如图，直线y=kx+b（k≠0）与x轴交于点（﹣4，0），则关于x的不等式kx+b＞0的解集是 ．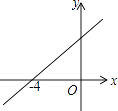

    查看试题解析

  • 13. 如图Rt△ABC中，∠ACB=90°，D为AB的中点，E在边AB上，AB=12，BC=6，当ED= 12 CD，则CE= ．

    查看试题解析

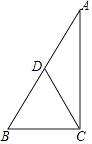  • 14. 如图，菱形OABC中，点A的坐标为（3，4），点C在x轴上，则点B的坐标是 ．

    查看试题解析

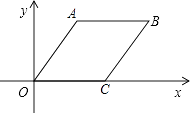  • 15. 如图，四边形ABCD是正方形，边长为4，点G在边BC上运动，DE⊥AG于E，BF∥DE交AG于点F，在运动过程中存在BF+EF的最小值，则这个最小值是 ．

    查看试题解析

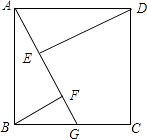  • 16. 在数学课上，老师提出如下问题：

    已知：如图， ΔABC 及AC边的中点O，

    求作：平行四边形ABCD

    小敏的作法如下：

    ①  连接BO并延长，在延长线上截取OD=BO

    ② 连接DA、DC，

    所以四边形ABCD就是所求作的平行四边形。


    老师说：”小敏的作法正确．“

    请回答：小敏的作法正确的理由是 ．

    查看试题解析

三、耐心做一做

  • 17. 计算：    
    (1)、18 ﹣ 32 + 12 ；
    (2)、（2 2 +3 3 ）2 ．

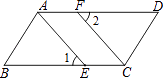
    查看试题解析

  • 18. 已知：如图，点E，F分别为▱ABCD的边BC，AD上的点，且∠1=∠2．

    求证：AE=CF．

    查看试题解析

  • 19. 已知：M（4，4），N（﹣2，﹣2），在横轴上存在点P，使PM=PN．求点P的坐标．

    查看试题解析

  • 20. 为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：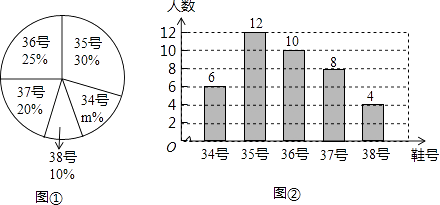

    (1)、本次接受随机抽样调查的学生人数为 ， 图①中m的值为；
    (2)、求本次调查获取的样本数据的众数和中位数；
    (3)、根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？

    查看试题解析

  • 21. 直线y=2x﹣2与x轴交于点A，与y轴交于点B．

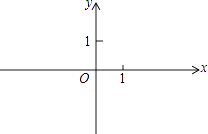    (1)、求点A、B的坐标；
    (2)、点C在x轴上，且S△ABC=3S△AOB ， 直接写出点C坐标．

    查看试题解析

  • 22. 五一节期间，电器市场火爆，某商店需要购进一批电视机和洗衣机，根据市场调查，电视机与洗衣机的进价和售价如下表：

    类别

    电视机

    洗衣机

    进价（元/台）

    1800

    1500

    售价（元/台）

    2000

    1600

    若该商店计划电视机和洗衣机共100台，设购进电视机x台，获得的总利润y元．

    (1)、求出y与x的函数关系；
    (2)、已知商店最多筹集资金161800元，求购进多少台电视机，才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多？并求出最多利润．（利润=售价﹣进价）

    查看试题解析

  • 23. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．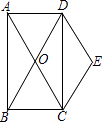

    (1)、求证：四边形OCED是菱形；
    (2)、若∠BAC=30°，AC=4，求菱形OCED的面积．

    查看试题解析

  • 24. 在菱形ABCD中，∠B=60°，AB=4，动点M以每秒1个单位的速度从点A出发运动到点B，点N以相同的速度从点B出发运动到点C，两点同时出发，过点M作MP⊥AB交直线CD于点P，连接NM、NP，设运动时间为t秒．

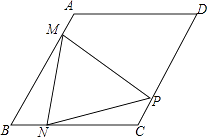    (1)、当t=2时，∠NMP=度；
    (2)、求t为何值时，以A、M、C、P为顶点的四边形是平行四边形；
    (3)、当△NPC为直角三角形时，求此时t的值．

    查看试题解析

  • 25. 问题：探究函数y=|x|﹣2的图象与性质．

    小华根据学习函数的经验，对函数y=|x|﹣2的图象与性质进行了探究．

    下面是小华的探究过程，请补充完整：

    (1)、在函数y=|x|﹣2中，自变量x可以是任意实数；

    如表是y与x的几组对应值．

    x

    …

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    …

    y

    …

    1

    0

    ﹣1

    ﹣2

    ﹣1

    0

    m

    …

    ①m=；

    ②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=；

    (2)、①如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；

    (3)、该函数的最小值为；
    (4)、已知直线 y1=12x−12 与函数y=|x|﹣2的图象交于C、D两点，当y1≥y时x的取值范围是 ．

    查看试题解析