江西省五市九校协作体2021届高三数学第一次联考试卷
试卷更新日期:2021-01-29 类型:高考模拟
一、单选题
-
1. 已知集合 , ,若 ,则实数a的取值范围为( )A、 B、 C、 D、2. 已知复数z满足 (i为虚数单位),则 ( 为z的共轭复数)在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. “ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件4. 为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由9位同学组成四个宣传小组,其中可回收物宣传小组有3位同学,餐厨垃圾、有害垃圾和其他垃圾宣传小组各有2位同学.现从这9位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )A、 B、 C、 D、5. 函数 的图象如图所示,为了得到 的图象,只需把 的图象上所有点( )
 A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个长度单位 D、向左平移 个长度单位6. 若x,y满足约束条件 ,则 的最小值为( )A、26 B、4 C、 D、-267. 蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x(每分钟鸣叫的次数)与气温y(单位: )存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y关于x的线性回归方程
A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个长度单位 D、向左平移 个长度单位6. 若x,y满足约束条件 ,则 的最小值为( )A、26 B、4 C、 D、-267. 蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x(每分钟鸣叫的次数)与气温y(单位: )存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y关于x的线性回归方程x(次数/分数)
20
30
40
50
60
y( )
25
27.5
29
32.5
36
则当蟋蟀每分钟鸣叫52次时,该地当时的气温预报值为( )
A、 B、 C、 D、8. 已知双曲线C: ( , )的左、右焦点分别为 , ,点P是C的右支上一点,连接 与y轴交于点M,若 (O为坐标原点), ,则双曲线C的离心率为( )A、 B、2 C、 D、39. 已知函数 是定义在 上的奇函数,对任意两个不相等的正数 ,都有 ,记 , , ,则( )A、 B、 C、 D、10. 如图,小方格是边长为1的小正方形,粗线画出的是某四棱锥的三视图,则该四棱锥的外接球表面积为( )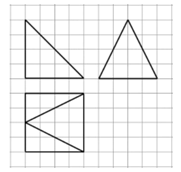 A、32π B、 C、41π D、11. 设 , ,O为坐标原点,点P满足 ,若直线 上存在点Q使得 ,则实数k的取值范围为( )A、 B、 C、 D、12. 已知函数 与函数 的图像上恰有两对关于 轴对称的点,则实数 的取值范围为( )A、 B、 C、 D、
A、32π B、 C、41π D、11. 设 , ,O为坐标原点,点P满足 ,若直线 上存在点Q使得 ,则实数k的取值范围为( )A、 B、 C、 D、12. 已知函数 与函数 的图像上恰有两对关于 轴对称的点,则实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 在 中, 与 的夹角为 , , , ,则14. 若正实数 ,满足 ,则 的最小值为.15. 数列 中, , ( ),则16. 已知正方体 的棱长为1,E,F,M分别为棱 , , 的中点,过点M与平面 平行的平面与 交于点N,则四面体 的体积为
三、解答题
-
17. 已知 的内角A,B,C的对边分别为a,b,c,且 .(1)、求角C的大小(2)、若 ,且 的面积为 ,求 的周长.18. 如图,已知四边形 为菱形,对角线 与 相交于O, ,平面 平面 直线 , 平面 ,
 (1)、求证: ;(2)、求二面角 的余弦值.19. 学校趣味运动会上增加了一项射击比赛,比赛规则如下:向A、B两个靶子进行射击,先向A靶射击一次,命中得1分,没有命中得0分;再向B靶连续射击两次,如果只命中一次得2分,一次也没有命中得0分,如果连续命中两次则得5分.甲同学准备参赛,经过一定的训练,甲同学的射击水平显著提高,目前的水平是:向A靶射击,命中的概率是 ;向B靶射击,命中的概率为 .假设甲同学每次射击结果相互独立.(1)、求甲同学恰好命中一次的概率;(2)、求甲同学获得的总分X的分布列及数学期望.20. 已知椭圆C: ( )过点 , , 为椭圆的左右顶点,且直线 , 的斜率的乘积为 .
(1)、求证: ;(2)、求二面角 的余弦值.19. 学校趣味运动会上增加了一项射击比赛,比赛规则如下:向A、B两个靶子进行射击,先向A靶射击一次,命中得1分,没有命中得0分;再向B靶连续射击两次,如果只命中一次得2分,一次也没有命中得0分,如果连续命中两次则得5分.甲同学准备参赛,经过一定的训练,甲同学的射击水平显著提高,目前的水平是:向A靶射击,命中的概率是 ;向B靶射击,命中的概率为 .假设甲同学每次射击结果相互独立.(1)、求甲同学恰好命中一次的概率;(2)、求甲同学获得的总分X的分布列及数学期望.20. 已知椭圆C: ( )过点 , , 为椭圆的左右顶点,且直线 , 的斜率的乘积为 . (1)、求椭圆C的方程;(2)、过右焦点F的直线l与椭圆C交于M,N两点,线段 的垂直平分线交直线l于点P,交直线 于点Q,求 的最小值.21. 已知函数 ,其中 .(1)、当 时,求函数 在 处的切线方程;(2)、记函数 的导函数是 ,若不等式 对任意的实数 恒成立,求实数 的取值范围;(3)、设函数 , 是函数 的导函数,若函数 存在两个极值点 , ,且 ,求实数 的取值范围.
(1)、求椭圆C的方程;(2)、过右焦点F的直线l与椭圆C交于M,N两点,线段 的垂直平分线交直线l于点P,交直线 于点Q,求 的最小值.21. 已知函数 ,其中 .(1)、当 时,求函数 在 处的切线方程;(2)、记函数 的导函数是 ,若不等式 对任意的实数 恒成立,求实数 的取值范围;(3)、设函数 , 是函数 的导函数,若函数 存在两个极值点 , ,且 ,求实数 的取值范围.