天津市西青区2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-01-29 类型：期末考试

进入出卷网下载

一、单选题

1. 已知全集 $U = {1, 2, 3, 4}$ ，集合 $A = {1, 2, 3}$ ， $B = {2, 3, 4}$ ，则 $∁_{U} (A \cap B) =$ （）

A、 ${2, 3}$ B、 ${1, 2, 3, 4}$ C、 ${1, 4}$ D、 ${2, 3, 4}$

查看试题解析
2. 下列四个函数中，在其定义域上既是奇函数又是递增函数的是（）

A、 $y = e^{x}$ B、 $y = \sin x$ C、 $y = \sqrt{x}$ D、 $y = x^{3}$

查看试题解析
3. 设 $a \in R$ ，则“ $a > 1$ ”是“ $a^{2} > a$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 下列说法正确的是（）

A、若 $a > b > 0$ ，则 $a c^{2} > b c^{2}$ B、若 $a > b$ ，则 $a^{2} > b^{2}$ C、若 $a < b < 0$ ，则 $a^{2} > a b > b^{2}$ D、若 $a < b$ ，则 $\frac{1}{a} > \frac{1}{b}$

查看试题解析
5. 设函数 $f (x) = \frac{1}{3} x - \ln x (x > 0) ，$ 则 $y = f (x)$ （）

A、在区间 $(\frac{1}{e} ， 1) ， (1 ， e)$ 内均有零点. B、在区间 $(\frac{1}{e} ， 1) ， (1 ， e)$ 内均无零点. C、在区间 $(\frac{1}{e} ， 1)$ 内无零点，在区间 $(1 ， e)$ 内有零点. D、在区间 $(\frac{1}{e} ， 1)$ 内有零点，在区间 $(1 ， e)$ 内无零点.

查看试题解析
6. 已知函数 $f (x) = \sin (x + \frac{π}{2}) + 1$ ，则（）

A、 $f (x)$ 是偶函数，最大值为1 B、 $f (x)$ 是偶函数，最大值为2 C、 $f (x)$ 是奇函数，最大值为1 D、 $f (x)$ 是奇函数，最大值为2

查看试题解析
7. 设 $a = \ln \frac{1}{2}$ ， $b = 2^{\frac{1}{e}}$ ， $c = e^{- 2}$ ，则 $a$ 、 $b$ 、 $c$ 的大小关系为（）

A、 $a < c < b$ B、 $a < b < c$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析
8. 对于函数 $f (x) = \sin (2 x + \frac{π}{6})$ ，下列命题
①函数图象关于直线 $x = - \frac{π}{12}$ 对称； ②函数图象关于点( $\frac{5 π}{12}$ ，0)对称；③函数图象可看作是把 $y = \sin 2 x$ 的图象向左平移个 $\frac{π}{6}$ 单位而得到；④函数图象可看作是把 $y = \sin (x + \frac{π}{6})$ 的图象上所有点的横坐标缩短到原来的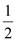倍 (纵坐标不变)而得到；其中正确的命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
9. 定义在R上的偶函数f（x）满足f（x+2）=f（x），且在[1，2]上是减函数，若α，β是锐角三角形的两个内角，则（）

A、f $(sinα) > f$ $(cos$ $β)$ B、f $(sinα) < f$ $(cos$ $β)$ C、f $(sin$ $α) > f$ $(sin$ $β)$ D、f $(cosα) < f$ $(cos$ $β)$

查看试题解析

二、填空题

10. 已知幂函数y=f（x）的图象过点（2， $\sqrt{2}$ ），则f（x）= ．

查看试题解析
11. $\log_{2} 3 \cdot \log_{3} 4 + {(\frac{27}{8})}^{\frac{1}{3}} + \sqrt{2 \times \sqrt[3]{8}} =$ .

查看试题解析
12. 命题“ $\forall x \in R$ ， $\exists n \in N^{*}$ ，使得 $n \geq x^{2}$ ”的否定形式是．

查看试题解析
13. 用长度为28米的篱笆围成一边靠墙的矩形花园，墙长为16米，则矩形花园面积的最大值是平方米.

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} 3 x^{2} + 2 (a - 1) x + 15 ， x \leq 1 \\ - 4 a + a \ln x ， x > 1 \end{array}$ ，若对任意的 $x_{1}$ 、 $x_{2} \in R$ ， $x_{1} \neq x_{2}$ ，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ 成立，则实数 $a$ 的取值范围是.

查看试题解析
15. 函数 $y = \tan x$ 的定义域为；若 $\tan x = 2$ ，则 $\frac{5 \cos x - \sin x}{\sin x + 2 \cos x} =$ .

查看试题解析

三、解答题

16. 已知 $α \in (\frac{π}{2}, π)$ ， $\sin α = \frac{3}{5}$ .

(1)、求 $\tan α$ 的值；

(2)、求 $\cos 2 α$ 的值；

(3)、若 $β \in [0, \frac{π}{2}]$ ， $\sin (α + β) = - \frac{5}{13}$ ，求 $\sin β$ .

查看试题解析
17. 若 $f (x) = a x^{2} - (a + 1) x + 1$ ， $a \in R$ .
（Ⅰ）若 $f (x) < 0$ 的解集为 $(\frac{1}{4}, 1)$ ，求 $a$ 的值；

（Ⅱ）求关于 $x$ 的不等式 $f (x) < 0$ 的解集.

查看试题解析
18. 已知函数 $y = \log_{a} x$ 过定点 $(m, n)$ ，函数 $f (x) = \frac{x}{x^{2} + m} + n$ 的定义域为 $[- 1, 1]$ .
（Ⅰ）求定点 $(m, n)$ 并证明函数 $f (x)$ 的奇偶性；

（Ⅱ）判断并证明函数 $f (x)$ 在 $[- 1, 1]$ 上的单调性；

（Ⅲ）解不等式 $f (2 x - 1) + f (x) < 0$ .

查看试题解析
19. 已知函数 $f (x) = 2 x^{2} - 3 x + 1$ .
（Ⅰ）函数 $h (x)$ 是奇函数，当 $x > 0$ 时， $h (x) = f (x)$ ，求 $h (x)$ 在 $x \in R$ 上的解析式；

（Ⅱ）若 $g (x) = - f (x) + m x + 1$ ，当 $x \in [1, 2]$ 时，若 $g (x)$ 的最大值为2，求 $m$ 的值.

查看试题解析
20. 已知函数 $f (x) = 4 \cos x \cdot \cos (x - \frac{π}{3}) + a$ .
（Ⅰ）求函数 $f (x)$ 的最小正周期；

（Ⅱ）求函数 $f (x)$ 在 $x \in [0 ， \frac{π}{2}]$ 上的单调递增区间；

（Ⅲ）若 $\frac{2 π}{3}$ 是函数 $f (x)$ 的一个零点，求实数 $a$ 的值及函数 $f (x)$ 在 $x \in [0 ， \frac{π}{2}]$ 上的值域.

查看试题解析